
題目列表(包括答案和解析)
(1)求P點的軌跡方程,并判斷P點的軌跡是怎樣的曲線;
(2)當λ=![]() 時,過點A1且斜率為1的直線與(1)中的曲線相交的另一點為B,能否在直線x=-9上找一點C,使△A1BC為正三角形.
時,過點A1且斜率為1的直線與(1)中的曲線相交的另一點為B,能否在直線x=-9上找一點C,使△A1BC為正三角形.
(1)求P點的軌跡方程,并判斷P點的軌跡是怎樣的曲線;
(2)當λ=![]() 時,過點A1且斜率為1的直線與(1)中的曲線相交的另一點為B,能否在直線x=-9上找一點C,使△A1BC為正三角形.
時,過點A1且斜率為1的直線與(1)中的曲線相交的另一點為B,能否在直線x=-9上找一點C,使△A1BC為正三角形.
在平面直角坐標系中,已知A1(-3,0),A2(3,0),P(x,y),M(![]() ,0),若實數λ使向量
,0),若實數λ使向量![]() ,λ
,λ![]() ,
,![]() 滿足λ2·(
滿足λ2·(![]() )2=
)2=![]() ·
·![]() .
.
(1)求點P的軌跡方程,并判斷P點的軌跡是怎樣的曲線;
(2)當λ=![]() 時,過點A1且斜率為1的直線與此時(1)中的曲線相交的另一點為B,能否在直線x=-9上找一點C,使ΔA1BC為正三角形(請說明理由).
時,過點A1且斜率為1的直線與此時(1)中的曲線相交的另一點為B,能否在直線x=-9上找一點C,使ΔA1BC為正三角形(請說明理由).
在平面直角坐標系中,已知A1(一3,0)、A2(3,0)、P(![]() 、y)、M(
、y)、M(![]() ,0),O為坐標原點,若實數
,0),O為坐標原點,若實數![]() 使向量
使向量![]() 、
、![]() 和
和![]() 滿足
滿足![]() =
=![]() ?
?![]() .
.
(1)求點P的軌跡方程,并判斷P點的軌跡是怎樣的曲線;
(2)當![]() 時,過點A1且斜率為1的直線與此時(1)中的曲線相交的另一個交點為B,能否在直線
時,過點A1且斜率為1的直線與此時(1)中的曲線相交的另一個交點為B,能否在直線![]() =-9上找到一點C,恰使△A1BC為正三角形?請說明理由.
=-9上找到一點C,恰使△A1BC為正三角形?請說明理由.
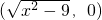 ,O為坐標原點,若實數λ使向量
,O為坐標原點,若實數λ使向量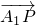 ,
,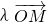 和
和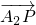 滿足:
滿足: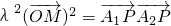 ,設點P的軌跡為W.
,設點P的軌跡為W.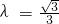 時,過點A1且斜率為1的直線與W相交的另一個交點為B,能否在直線x=-9上找到一點C,恰使△A1BC為正三角形?請說明理由.
時,過點A1且斜率為1的直線與W相交的另一個交點為B,能否在直線x=-9上找到一點C,恰使△A1BC為正三角形?請說明理由.一、選擇題:
1.C 2.D 3.C 4.A 5.B 6.C 7.B 8.A 9.D 10.A 11.A 12.C
二、填空題:
13..files/image250.gif) 14. 26 15. -3 16.
14. 26 15. -3 16. .files/image252.gif) 17. 3
18.
17. 3
18. .files/image254.gif)
19..files/image256.gif) 20.(0,1) 21.
20.(0,1) 21. .files/image258.gif) 22.
22..files/image260.gif) 23.765 24.5
23.765 24.5
25.2
26..files/image262.gif)
三、解答題:
27、解:(1)∵cos3x=4cos3x-3cosx,則.files/image193.gif) =4cos2x-3=2cos2x-1
=4cos2x-3=2cos2x-1
∴f(x)=2cos2x-1+2sin2x
=2.files/image265.gif) sin(2x+
sin(2x+.files/image242.gif) )-1
)-1
在2x+.files/image242.gif) =2kπ+
=2kπ+.files/image269.gif) 時,f(x)取得最大值2
時,f(x)取得最大值2.files/image265.gif) -1
-1
即在x=kπ+.files/image271.gif) (k∈Z)時,f(x)取得最大值2
(k∈Z)時,f(x)取得最大值2.files/image265.gif) -1
-1
(2)∵f(x)=2.files/image265.gif) sin(2x+
sin(2x+.files/image242.gif) )-1
)-1
要使f(x)遞減,x滿足2kπ+.files/image269.gif) ≤2x+
≤2x+.files/image242.gif) ≤2kπ+
≤2kπ+.files/image274.gif)
即kπ+.files/image271.gif) ≤x≤kπ+
≤x≤kπ+.files/image277.gif) (k∈Z)
(k∈Z)
又∵cosx≠0,即x≠kπ+.files/image269.gif) (k∈Z)
(k∈Z)
|