)
28、解:(1)p(ξ個正面向上,4-ξ個背面向上的概率,其中ξ可能取值為0,1,2,3,4。
∴p(ξ=0)= 學沖刺階段每日綜合模擬一練(4).files/image284.gif) (1-
(1-學沖刺階段每日綜合模擬一練(4).files/image020.gif) )2
)2學沖刺階段每日綜合模擬一練(4).files/image284.gif) (1-a)2=
(1-a)2=學沖刺階段每日綜合模擬一練(4).files/image287.gif) (1-a)2
(1-a)2
p(ξ=1)= 學沖刺階段每日綜合模擬一練(4).files/image289.gif)
學沖刺階段每日綜合模擬一練(4).files/image020.gif) (1-
(1-學沖刺階段每日綜合模擬一練(4).files/image020.gif) )
)學沖刺階段每日綜合模擬一練(4).files/image284.gif) (1-a)2+
(1-a)2+學沖刺階段每日綜合模擬一練(4).files/image284.gif) (1-
(1-學沖刺階段每日綜合模擬一練(4).files/image020.gif) )2?
)2?學沖刺階段每日綜合模擬一練(4).files/image289.gif) a(1-a)=
a(1-a)=
學沖刺階段每日綜合模擬一練(4).files/image020.gif) (1-a)
(1-a)
p(ξ=2)= 學沖刺階段每日綜合模擬一練(4).files/image291.gif) (
(學沖刺階段每日綜合模擬一練(4).files/image020.gif) )2
)2學沖刺階段每日綜合模擬一練(4).files/image284.gif) (1-a)2+
(1-a)2+學沖刺階段每日綜合模擬一練(4).files/image289.gif)
學沖刺階段每日綜合模擬一練(4).files/image020.gif) (1-
(1-學沖刺階段每日綜合模擬一練(4).files/image020.gif) )
)學沖刺階段每日綜合模擬一練(4).files/image289.gif) a(1-a)+
a(1-a)+
學沖刺階段每日綜合模擬一練(4).files/image284.gif) (1-
(1-學沖刺階段每日綜合模擬一練(4).files/image020.gif) )2?
)2?學沖刺階段每日綜合模擬一練(4).files/image291.gif) a2=
a2=學沖刺階段每日綜合模擬一練(4).files/image287.gif) (1+2a-2 a2)
(1+2a-2 a2)
p(ξ=3)= 學沖刺階段每日綜合模擬一練(4).files/image291.gif) (
(學沖刺階段每日綜合模擬一練(4).files/image020.gif) )2
)2學沖刺階段每日綜合模擬一練(4).files/image289.gif) a(1-a)+
a(1-a)+
學沖刺階段每日綜合模擬一練(4).files/image289.gif)
學沖刺階段每日綜合模擬一練(4).files/image020.gif) (1-
(1-學沖刺階段每日綜合模擬一練(4).files/image020.gif) )
)學沖刺階段每日綜合模擬一練(4).files/image291.gif) a2=
a2=學沖刺階段每日綜合模擬一練(4).files/image295.gif)
p(ξ=4)= 學沖刺階段每日綜合模擬一練(4).files/image291.gif) (
(學沖刺階段每日綜合模擬一練(4).files/image020.gif) )2
)2學沖刺階段每日綜合模擬一練(4).files/image291.gif) a2=
a2=學沖刺階段每日綜合模擬一練(4).files/image287.gif) a2
a2
(2) ∵0<a<1,∴p(ξ=1) <p(ξ=1),p(ξ=4) <p(ξ=3)
則p(ξ=2)- p(ξ=1)= 學沖刺階段每日綜合模擬一練(4).files/image287.gif) (1+2a-2 a2)-
(1+2a-2 a2)-
學沖刺階段每日綜合模擬一練(4).files/image297.gif) =-
=-學沖刺階段每日綜合模擬一練(4).files/image299.gif) ≥0
≥0
由學沖刺階段每日綜合模擬一練(4).files/image301.gif)
學沖刺階段每日綜合模擬一練(4).files/image303.gif) ,即a∈[
,即a∈[學沖刺階段每日綜合模擬一練(4).files/image305.gif) ]
]
(3)由(1)知ξ的數(shù)學期望為
Eξ=0×學沖刺階段每日綜合模擬一練(4).files/image307.gif) (1-a)2+1×
(1-a)2+1×學沖刺階段每日綜合模擬一練(4).files/image309.gif) (1-a)+2×
(1-a)+2×學沖刺階段每日綜合模擬一練(4).files/image307.gif) (1+2a-2a2)+3×
(1+2a-2a2)+3×學沖刺階段每日綜合模擬一練(4).files/image295.gif) +4×
+4×學沖刺階段每日綜合模擬一練(4).files/image313.gif) =2a+1
=2a+1
29、解:(1)∵EF∥CD∥AB,EG∥PB,根據(jù)面面平行的判定定理
∴平面EFG∥平面PAB,又PA學沖刺階段每日綜合模擬一練(4).files/image315.gif) 面PAB,∴AP∥平面EFG
面PAB,∴AP∥平面EFG
(2)∵平面PDC⊥平面ABCD,AD⊥DC
∴AD⊥平面PCD,而BC∥AD,∴BC⊥面EFD
過C作CR⊥EF交EF延長線于R點連GR,根據(jù)三垂線定理知
∠GRC即為二面角的平面角,∵GC=CR,∴∠GRC=45°,
故二面角G-EF-D的大小為45°。
(3)Q點為PB的中點,取PC中點M,則QM∥BC,∴QM⊥PC
在等腰Rt△PDC中,DM⊥PC,∴PC⊥面ADMQ
30、解:(1)由已知可得,學沖刺階段每日綜合模擬一練(4).files/image317.gif) =(x+3,y),
=(x+3,y),學沖刺階段每日綜合模擬一練(4).files/image319.gif) =(x-3,y),
=(x-3,y),學沖刺階段每日綜合模擬一練(4).files/image321.gif) =(
=(學沖刺階段每日綜合模擬一練(4).files/image323.gif) ,0),
,0),
∵學沖刺階段每日綜合模擬一練(4).files/image135.gif) 2(
2(學沖刺階段每日綜合模擬一練(4).files/image321.gif) )2=
)2=學沖刺階段每日綜合模擬一練(4).files/image317.gif) ?
?學沖刺階段每日綜合模擬一練(4).files/image319.gif) ,∴
,∴學沖刺階段每日綜合模擬一練(4).files/image135.gif) 2(x2-9)=x2-9+y2,
2(x2-9)=x2-9+y2,
即P點的軌跡方程(1-學沖刺階段每日綜合模擬一練(4).files/image135.gif) 2)x2+y2=9(1-
2)x2+y2=9(1-學沖刺階段每日綜合模擬一練(4).files/image135.gif) 2)
2)
當1-學沖刺階段每日綜合模擬一練(4).files/image135.gif) 2>0,且
2>0,且學沖刺階段每日綜合模擬一練(4).files/image135.gif) ≠0,即
≠0,即學沖刺階段每日綜合模擬一練(4).files/image135.gif) ∈(-1,0)時,有
∈(-1,0)時,有學沖刺階段每日綜合模擬一練(4).files/image327.gif) +
+學沖刺階段每日綜合模擬一練(4).files/image329.gif) =1,
=1,
∵1-學沖刺階段每日綜合模擬一練(4).files/image135.gif) 2>0,∴
2>0,∴學沖刺階段每日綜合模擬一練(4).files/image329.gif) >0,∴x2≤9。
>0,∴x2≤9。
∴P點的軌跡是點A1,(-3,0)與點A2(3,0)
當學沖刺階段每日綜合模擬一練(4).files/image135.gif) =0時,方程為x2+y2=9,P的軌跡是點A1(-3,0)與點A2(3,0)
=0時,方程為x2+y2=9,P的軌跡是點A1(-3,0)與點A2(3,0)
當1-學沖刺階段每日綜合模擬一練(4).files/image135.gif) 2<0,即入∈(-∞,-1)∪(1,+∞)時,方程為
2<0,即入∈(-∞,-1)∪(1,+∞)時,方程為學沖刺階段每日綜合模擬一練(4).files/image327.gif) -
-學沖刺階段每日綜合模擬一練(4).files/image329.gif) =1,P點的軌跡是雙曲線。
=1,P點的軌跡是雙曲線。
當1-學沖刺階段每日綜合模擬一練(4).files/image135.gif) 2=0,即
2=0,即學沖刺階段每日綜合模擬一練(4).files/image135.gif) =±1時,方程為y=0,P點的軌跡是射線。
=±1時,方程為y=0,P點的軌跡是射線。
(2)過點A1且斜率為1的直線方程為y=x+3,
當學沖刺階段每日綜合模擬一練(4).files/image135.gif) =
=學沖刺階段每日綜合模擬一練(4).files/image333.gif) 時,曲線方程為
時,曲線方程為學沖刺階段每日綜合模擬一練(4).files/image327.gif) +
+學沖刺階段每日綜合模擬一練(4).files/image335.gif) =1,
=1,
由(1)知,其軌跡為點A1(-3,0)與A2(3,0)
因直線過A1(-3,0),但不過A2(3,0)。
所以,點B不存在。
所以,在直線x=-9上找不到點C滿足條件。
31、解:(理)(1)f′(x)=-學沖刺階段每日綜合模擬一練(4).files/image337.gif) +a=
+a=學沖刺階段每日綜合模擬一練(4).files/image339.gif)
(i)若a=0時,f′(x)= 學沖刺階段每日綜合模擬一練(4).files/image341.gif) >0
>0學沖刺階段每日綜合模擬一練(4).files/image343.gif) x>0,f′(x)<0
x>0,f′(x)<0學沖刺階段每日綜合模擬一練(4).files/image343.gif) x<0
x<0
∴f(x)在(0,+∞)單調遞增,在(-∞,0)單調遞減。
(ii)若學沖刺階段每日綜合模擬一練(4).files/image346.gif) 時,f′(x)≤0對x∈R恒成立。
時,f′(x)≤0對x∈R恒成立。
∴f(x)在R上單調遞減。
(iii)若-1<a<0,由f′(x)>0學沖刺階段每日綜合模擬一練(4).files/image343.gif) ax2+2x+a>0
ax2+2x+a>0學沖刺階段每日綜合模擬一練(4).files/image343.gif)
學沖刺階段每日綜合模擬一練(4).files/image350.gif) <x<
<x<學沖刺階段每日綜合模擬一練(4).files/image352.gif)
由f′(x)<0可得x>學沖刺階段每日綜合模擬一練(4).files/image352.gif) 或x<
或x<學沖刺階段每日綜合模擬一練(4).files/image350.gif)
∴f(x)在[學沖刺階段每日綜合模擬一練(4).files/image350.gif) ,
,學沖刺階段每日綜合模擬一練(4).files/image352.gif) ]單調遞增
]單調遞增
在(-∞,學沖刺階段每日綜合模擬一練(4).files/image350.gif) ],[
],[學沖刺階段每日綜合模擬一練(4).files/image352.gif)
學沖刺階段每日綜合模擬一練(4).files/image354.gif) 上單調遞減。
上單調遞減。
綜上所述:若a≤-1時,f(x)在(-∞,+∞)上單調遞減。
(2)由(1)當a=-1時,f(x)在(-∞,+∞)上單調遞減。
當x∈(0,+∞)時f(x)<f(0)
∴l(xiāng)n(1+x2)-x<0 即ln(1+x2)<x
∴l(xiāng)n[(1+學沖刺階段每日綜合模擬一練(4).files/image356.gif) )(1+
)(1+學沖刺階段每日綜合模擬一練(4).files/image358.gif) )……(1+
)……(1+學沖刺階段每日綜合模擬一練(4).files/image360.gif) )]
)]
=ln[(1+學沖刺階段每日綜合模擬一練(4).files/image356.gif) )(1+
)(1+學沖刺階段每日綜合模擬一練(4).files/image358.gif) )+…ln(1+
)+…ln(1+學沖刺階段每日綜合模擬一練(4).files/image360.gif) )<
)<學沖刺階段每日綜合模擬一練(4).files/image362.gif) +
+學沖刺階段每日綜合模擬一練(4).files/image364.gif) +…+
+…+學沖刺階段每日綜合模擬一練(4).files/image366.gif)
<學沖刺階段每日綜合模擬一練(4).files/image368.gif) =1-
=1-學沖刺階段每日綜合模擬一練(4).files/image370.gif) +
+學沖刺階段每日綜合模擬一練(4).files/image370.gif) -
-學沖刺階段每日綜合模擬一練(4).files/image373.gif) +…+
+…+學沖刺階段每日綜合模擬一練(4).files/image375.gif) =1-
=1-學沖刺階段每日綜合模擬一練(4).files/image377.gif) <1
<1
∴(1+學沖刺階段每日綜合模擬一練(4).files/image356.gif) )(1+
)(1+學沖刺階段每日綜合模擬一練(4).files/image358.gif) )……(1+
)……(1+學沖刺階段每日綜合模擬一練(4).files/image360.gif) )<e
)<e
32、解:(1)由題可知:學沖刺階段每日綜合模擬一練(4).files/image379.gif) 與函數(shù)
與函數(shù)學沖刺階段每日綜合模擬一練(4).files/image381.gif) 互為反函數(shù),所以,
互為反函數(shù),所以,
學沖刺階段每日綜合模擬一練(4).files/image383.gif) ,
,學沖刺階段每日綜合模擬一練(4).files/image385.gif) (2)因為點
(2)因為點學沖刺階段每日綜合模擬一練(4).files/image387.gif) 在函數(shù)
在函數(shù)學沖刺階段每日綜合模擬一練(4).files/image389.gif) 的圖像上,所以,
的圖像上,所以,學沖刺階段每日綜合模擬一練(4).files/image391.gif)
學沖刺階段每日綜合模擬一練(4).files/image393.gif)
在上式中令學沖刺階段每日綜合模擬一練(4).files/image395.gif) 可得:
可得:學沖刺階段每日綜合模擬一練(4).files/image397.gif) ,又因為:
,又因為:學沖刺階段每日綜合模擬一練(4).files/image399.gif) ,
,學沖刺階段每日綜合模擬一練(4).files/image401.gif) ,代入可解得:
,代入可解得:學沖刺階段每日綜合模擬一練(4).files/image403.gif) .所以,
.所以,學沖刺階段每日綜合模擬一練(4).files/image405.gif) ,(*)式可化為:
,(*)式可化為:學沖刺階段每日綜合模擬一練(4).files/image407.gif)
學沖刺階段每日綜合模擬一練(4).files/image393.gif) ①
①
(3)直線學沖刺階段每日綜合模擬一練(4).files/image244.gif) 的方程為:
的方程為:學沖刺階段每日綜合模擬一練(4).files/image410.gif) ,
,學沖刺階段每日綜合模擬一練(4).files/image393.gif) ,
,
在其中令學沖刺階段每日綜合模擬一練(4).files/image412.gif) ,得
,得學沖刺階段每日綜合模擬一練(4).files/image414.gif) ,又因為
,又因為學沖刺階段每日綜合模擬一練(4).files/image244.gif) 在y軸上的截距為
在y軸上的截距為學沖刺階段每日綜合模擬一練(4).files/image416.gif) ,所以,
,所以,
學沖刺階段每日綜合模擬一練(4).files/image418.gif) =
=學沖刺階段每日綜合模擬一練(4).files/image416.gif) ,結合①式可得:
,結合①式可得:學沖刺階段每日綜合模擬一練(4).files/image420.gif) ②
②
由①可知:當自然數(shù)學沖刺階段每日綜合模擬一練(4).files/image422.gif) 時,
時,學沖刺階段每日綜合模擬一練(4).files/image424.gif) ,
,學沖刺階段每日綜合模擬一練(4).files/image426.gif) ,
,
兩式作差得:學沖刺階段每日綜合模擬一練(4).files/image428.gif) .
.
結合②式得:學沖刺階段每日綜合模擬一練(4).files/image430.gif)
學沖刺階段每日綜合模擬一練(4).files/image432.gif) ③
③
在③中,令學沖刺階段每日綜合模擬一練(4).files/image434.gif) ,結合
,結合學沖刺階段每日綜合模擬一練(4).files/image399.gif) ,可解得:
,可解得:學沖刺階段每日綜合模擬一練(4).files/image437.gif) ,
,
又因為:當學沖刺階段每日綜合模擬一練(4).files/image422.gif) 時,
時,學沖刺階段每日綜合模擬一練(4).files/image440.gif) ,所以,舍去
,所以,舍去學沖刺階段每日綜合模擬一練(4).files/image442.gif) ,得
,得學沖刺階段每日綜合模擬一練(4).files/image444.gif) .
.
同上,在③中,依次令學沖刺階段每日綜合模擬一練(4).files/image446.gif) ,可解得:
,可解得:學沖刺階段每日綜合模擬一練(4).files/image448.gif) ,
,學沖刺階段每日綜合模擬一練(4).files/image450.gif) .
.
猜想:學沖刺階段每日綜合模擬一練(4).files/image452.gif)
學沖刺階段每日綜合模擬一練(4).files/image454.gif) .下用數(shù)學歸納法證明.
.下用數(shù)學歸納法證明.
(1)學沖刺階段每日綜合模擬一練(4).files/image456.gif) 時,由已知條件及上述求解過程知顯然成立.
時,由已知條件及上述求解過程知顯然成立.
(2)假設學沖刺階段每日綜合模擬一練(4).files/image458.gif) 時命題成立,即
時命題成立,即學沖刺階段每日綜合模擬一練(4).files/image460.gif)
學沖刺階段每日綜合模擬一練(4).files/image462.gif) ,則由③式可得:
,則由③式可得:學沖刺階段每日綜合模擬一練(4).files/image464.gif)
把學沖刺階段每日綜合模擬一練(4).files/image460.gif) 代入上式并解方程得:
代入上式并解方程得:學沖刺階段每日綜合模擬一練(4).files/image466.gif)
由于學沖刺階段每日綜合模擬一練(4).files/image468.gif) ,所以,
,所以,學沖刺階段每日綜合模擬一練(4).files/image470.gif) ,所以,
,所以,學沖刺階段每日綜合模擬一練(4).files/image472.gif)
符合題意,應舍去,故只有學沖刺階段每日綜合模擬一練(4).files/image474.gif) .
.
所以,學沖刺階段每日綜合模擬一練(4).files/image476.gif) 時命題也成立.
時命題也成立.
綜上可知:數(shù)列學沖刺階段每日綜合模擬一練(4).files/image168.gif) 的通項公式為
的通項公式為學沖刺階段每日綜合模擬一練(4).files/image452.gif)
學沖刺階段每日綜合模擬一練(4).files/image454.gif)

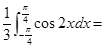
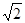 D.
D.
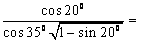
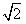
![]()
![]() D.
D.![]()
![]() =
= ![]() D.―2
D.―2 =
=學沖刺階段每日綜合模擬一練(4).files/image250.gif) 14. 26 15. -3 16.
14. 26 15. -3 16. 學沖刺階段每日綜合模擬一練(4).files/image252.gif) 17. 3
18.
17. 3
18. 學沖刺階段每日綜合模擬一練(4).files/image254.gif)
學沖刺階段每日綜合模擬一練(4).files/image256.gif) 20.(0,1) 21.
20.(0,1) 21. 學沖刺階段每日綜合模擬一練(4).files/image258.gif) 22.
22.學沖刺階段每日綜合模擬一練(4).files/image260.gif) 23.765 24.5
23.765 24.5 學沖刺階段每日綜合模擬一練(4).files/image262.gif)
學沖刺階段每日綜合模擬一練(4).files/image193.gif) =4cos2x-3=2cos2x-1
=4cos2x-3=2cos2x-1學沖刺階段每日綜合模擬一練(4).files/image265.gif) sin(2x+
sin(2x+學沖刺階段每日綜合模擬一練(4).files/image242.gif) )-1
)-1
學沖刺階段每日綜合模擬一練(4).files/image242.gif) =2kπ+
=2kπ+學沖刺階段每日綜合模擬一練(4).files/image269.gif) 時,f(x)取得最大值2
時,f(x)取得最大值2學沖刺階段每日綜合模擬一練(4).files/image265.gif) -1
-1學沖刺階段每日綜合模擬一練(4).files/image271.gif) (k∈Z)時,f(x)取得最大值2
(k∈Z)時,f(x)取得最大值2學沖刺階段每日綜合模擬一練(4).files/image265.gif) -1
-1 學沖刺階段每日綜合模擬一練(4).files/image265.gif) sin(2x+
sin(2x+學沖刺階段每日綜合模擬一練(4).files/image242.gif) )-1
)-1學沖刺階段每日綜合模擬一練(4).files/image269.gif) ≤2x+
≤2x+學沖刺階段每日綜合模擬一練(4).files/image242.gif) ≤2kπ+
≤2kπ+學沖刺階段每日綜合模擬一練(4).files/image274.gif)
學沖刺階段每日綜合模擬一練(4).files/image271.gif) ≤x≤kπ+
≤x≤kπ+學沖刺階段每日綜合模擬一練(4).files/image277.gif) (k∈Z)
(k∈Z)學沖刺階段每日綜合模擬一練(4).files/image269.gif) (k∈Z)
(k∈Z)