
�}Ŀ�б�(�����𰸺ͽ���)
 ��
�� ��
�� �鳣��(sh��)���x���ʞ�
�鳣��(sh��)���x���ʞ� ���p����
���p���� ��
�� �ϵĄ�(d��ng)�c(di��n)
�ϵĄ�(d��ng)�c(di��n) ���ɽ��c(di��n)�ľ��x֮�͵���Сֵ��
���ɽ��c(di��n)�ľ��x֮�͵���Сֵ�� �����タ
�����タ ��
��
 �Ľ��c(di��n)�c�p����
�Ľ��c(di��n)�c�p���� ��һ��c(di��n)�غϡ�(��)���タ
��һ��c(di��n)�غϡ�(��)���タ �ķ��̣������^(gu��)ֱ��
�ķ��̣������^(gu��)ֱ�� ��
�� ��
�� ��ؓ(f��)����(sh��)��������һ�c(di��n)
��ؓ(f��)����(sh��)��������һ�c(di��n) ���タ
���タ ���ɗl�о������c(di��n)�քe��
���ɗl�о������c(di��n)�քe�� ��
�� ������(bi��o)ԭ�c(di��n)
������(bi��o)ԭ�c(di��n) ������
������ ��ֱ���ĈA��(n��i)����(sh��)��(sh��)
��ֱ���ĈA��(n��i)����(sh��)��(sh��) ��ȡֵ������
��ȡֵ������
����������һ��(w��n)����������֪���p���������� ���x���ʞ�
���x���ʞ� ���t�L(zh��ng)�S�L(zh��ng)��2�����p����������c(di��n)��
���t�L(zh��ng)�S�L(zh��ng)��2�����p����������c(di��n)�� ������?hu��)��タ
������?hu��)��タ �ķ���
�ķ���
�ڶ���(w��n)�У� ��
�� ��
�� ��
�� ��
��
��ֱ�� �ķ��̞�
�ķ��̞� ����
���� ��
��
���� ��ͬ���ɵã�
��ͬ���ɵã�
�����ڸ��cϵ��(sh��)���P(gu��n)ϵ�õ��� ��
�� �Ƿ���
�Ƿ��� �ăɂ�(g��)��ͬ�ĸ�������
�ăɂ�(g��)��ͬ�ĸ�������
����֪�� ����
����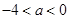
�⣺(��)����֪���p���������� ���x���ʞ�
���x���ʞ� ���t�L(zh��ng)�S�L(zh��ng)��2�����p����������c(di��n)��
���t�L(zh��ng)�S�L(zh��ng)��2�����p����������c(di��n)�� ������?hu��)��タ
������?hu��)��タ �ķ���
�ķ���
�����O(sh��) ��
�� ��
�� ��
�� ��
��
��ֱ�� �ķ��̞�
�ķ��̞� ����
���� ��
��
���� ��ͬ���ɵã�
��ͬ���ɵã� ��
��
�� ��
�� �Ƿ���
�Ƿ��� �ăɂ�(g��)��ͬ�ĸ�������
�ăɂ�(g��)��ͬ�ĸ�������
����֪�� ����
����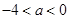
| 10-x |
| 10+x |
| 10-x |
| 10+x |
��֪����(sh��) ��
�� ȡ�ØOֵ
ȡ�ØOֵ
��1���� ���{(di��o)�^(q��)�g����
�Ć��{(di��o)�^(q��)�g���� ��ʾ����
��ʾ����
��2���O(sh��) ��
�� ��������
�������� ��ʹ��
��ʹ�� ��������
�������� ��ȡֵ����.
��ȡֵ����.
����������һ��(w��n)����

����(j��)�}�� ��
�� ȡ�ØOֵ,
ȡ�ØOֵ, 
��(du��)����(sh��)a����rӑՓ����֪
��(d��ng) ��
�� �r(sh��)�f���^(q��)�g:
�r(sh��)�f���^(q��)�g:  �f�p�^(q��)�g:
�f�p�^(q��)�g:  ,
,

��(d��ng) ��
�� �r(sh��)�f���^(q��)�g:
�r(sh��)�f���^(q��)�g:  �f�p�^(q��)�g:
�f�p�^(q��)�g:  ,
,

�ڶ���(w��n)�У� ��(1)֪:
��(1)֪:  ��
�� ��
��

 ��
��
 ��
��


�Ķ���⡣
��: 
 ��..3��
��..3��
 ��
�� ȡ�ØOֵ,
ȡ�ØOֵ,  ����������������..4��
����������������..4��
(1) ��(d��ng) ��
�� �r(sh��) �f���^(q��)�g:
�r(sh��) �f���^(q��)�g:  �f�p�^(q��)�g:
�f�p�^(q��)�g:  ,
,

��(d��ng) ��
�� �r(sh��)�f���^(q��)�g:
�r(sh��)�f���^(q��)�g:  �f�p�^(q��)�g:
�f�p�^(q��)�g:  ,
,
 ��������.6��
��������.6��
(2)  ��(1)֪:
��(1)֪:  ��
�� ��
��

 ��
��
 ��
��

 ������������.10��
������������.10��
 , ʹ
, ʹ ����
����



 ��:
��: 
�м�(x��)��x���憖(w��n)�}�Ľⷨ��
�O(sh��)A=[0, 1],������ʽ21-x-a��0��A���н�,��(sh��)��(sh��)a��ȡֵ������
�⣺����֪�ɵ� a �� 21-x
��f(x)= 21-x ,�߲���ʽa ��21-x��A���н�,
��a ��f(x)��A�ϵ����ֵ.
��f(x)��[0,1]�φ��{(di��o)�f�p��f(x)max =f(0)=2. ����(sh��)��(sh��)a��ȡֵ������a��2.
�о��W(xu��)��(x��)���φ�(w��n)�}�Ľⷨ��Ո(q��ng)��Q����Ć�(w��n)�}��
(1)��֪����(sh��)f(x)=x2+2x+3(-2��x��-1)����f(x)�ķ�����(sh��)��������(sh��)�Ķ��x��A��
(2)��(du��)��(1)�е�A���O(sh��)g(x)=![]() ��x��A,ԇ�Д�g(x)�Ć��{(di��o)��(��(xi��)�����ɣ������C��)��
��x��A,ԇ�Д�g(x)�Ć��{(di��o)��(��(xi��)�����ɣ������C��)��
(3)��B ={x|![]() ��2x+a�C5}���Ҍ�(du��)��(1)�е�A��A��B��F����(sh��)��(sh��)a��ȡֵ������
��2x+a�C5}���Ҍ�(du��)��(1)�е�A��A��B��F����(sh��)��(sh��)a��ȡֵ������
 x��A��ԇ�Д�g��x���Ć��{(di��o)�ԣ������C��
x��A��ԇ�Д�g��x���Ć��{(di��o)�ԣ������C�� ��2x+a-5}����A��B�٦�����(sh��)��(sh��)a��ȡֵ������
��2x+a-5}����A��B�٦�����(sh��)��(sh��)a��ȡֵ�������ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com