日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

已知直三棱柱中, , ， 是和的交點, 若.

（1）求的長；  （2）求點到平面的距離；

（3）求二面角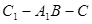的平面角的正弦值的大小.

【解析】本試題主要考查了距離和角的求解運用。第一問中，利用ACCA為正方形, AC=3

第二問中，利用面BBCC內作CDBC, 則CD就是點C平面ABC的距離CD=，第三問中，利用三垂線定理作二面角的平面角，然后利用直角三角形求解得到其正弦值為

解法一: (1)連AC交AC于E, 易證ACCA為正方形, AC=3 ……………  5分

(2)在面BBCC內作CDBC, 則CD就是點C平面ABC的距離CD= … 8分

(3) 易得AC面ACB, 過E作EHAB于H, 連HC, 則HCAB

CHE為二面角C－AB－C的平面角. ………  9分

sinCHE=二面角C－AB－C的平面角的正弦大小為 ……… 12分

解法二: (1)分別以直線CB、CC、CA為x、y為軸建立空間直角坐標系, 設|CA|=h, 則C(0, 0, 0), B(4, 0, 0), B(4, －3, 0), C(0, －3, 0), A(0, 0, h), A(0, －3, h), G(2, －, －) ………………………  3分

=(2, －, －), =(0, －3, －h(huán))  ……… 4分

·=0,  h=3

(2)設平面ABC得法向量=(a, b, c),則可求得=(3, 4, 0) (令a=3)

點A到平面ABC的距離為H=||=……… 8分

(3) 設平面ABC的法向量為=(x, y, z),則可求得=(0, 1, 1) (令z=1)

二面角C－AB－C的大小滿足cos== ………  11分

二面角C－AB－C的平面角的正弦大小為