
2008年安徽淮北西園中學中考第二次模擬考試
數學試卷
一、選擇題(本題共10小題,每小題4分,滿分40分)
A.±4 B
2,
3,把不等式組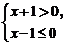 的解集表示在數軸上,如圖1,正確的是( )
的解集表示在數軸上,如圖1,正確的是( )

4,2008中國(淮北)專利技術推介會在我市隆重開幕,下(左)圖2是會展中心搭成的展臺,圖中所示展臺的主視圖是( )
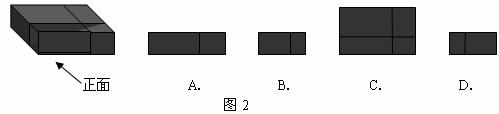
5,如圖3,把一個長方形紙片沿EF折疊后,點D、C分別落在D′、C′的位置,若∠EFB=65°,則∠AED′等于( )
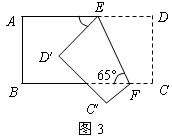
A.50° B.55° C.60° D.65°
6,如圖4,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,請按照圖中所標注的數據,計算圖中實線所圍成的圖形的面積S是( )
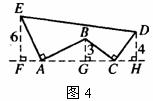
A.50 B
7,已知:如圖5,點G是BC的中點,點H在AF上,動點P以每秒
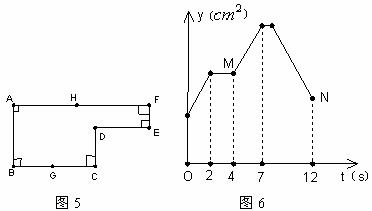
A.1個 B.2個 C.3個 D.4個
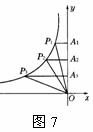
8,如圖7,P1、P2、P3是雙曲線上的三點.過這三點分別作y軸的垂線,得到三個三角形△P
A.S1<S2<S3 B.S2<S1<S
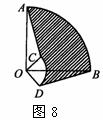
9,如圖8,圓心角都是90°的扇形OAB與扇形OCD疊放在一起,OA=3,OC=1,分別連結AC、BD,則圖中陰影部分的面積為( )
A.  B.
B. 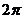 C.
C. 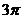 D.
D. 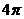
二、填空題(本題共4小題,每小題5分,滿分20分)
11,某住宅小區6月份隨機抽查了該小區6天的用水量(單位:噸),結果分別是30、34、32、37、28、31,那么,請你估計該小區6月份(30天)的總用水量約是 噸.
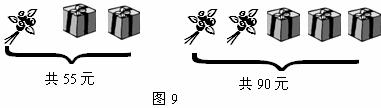
12、母親節那天,很多同學給媽媽準備了鮮花和禮盒.從如圖9中信息可知一束鮮花的價格是___元.
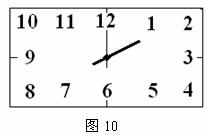
13,如圖10為長方形時鐘鐘面示意圖,時鐘的中心在長方形對角線的交點上,長方形的寬為20厘米,鐘面數字2在長方形的頂點處,則長方形的長為___厘米.
14,在數學中,為了簡便,記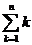 =1+2+3+…+(n-1)+ n.1!=1,2!=2×1,3!=3×2×1,…,n!=n×(n-1)×(n-2)×…×3×2×1.則
=1+2+3+…+(n-1)+ n.1!=1,2!=2×1,3!=3×2×1,…,n!=n×(n-1)×(n-2)×…×3×2×1.則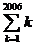 -
-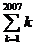 +
+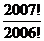 =___.
=___.
三、(本題共2小題,每小題8分,滿分16分)
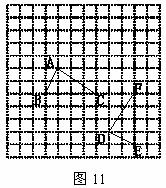
(1)圖中的格點△DEF是由格點△ABC通過怎樣的變換得到的?(寫出變換過程)
(2)根據你寫出的變換過程,求出點A經過的路線長。
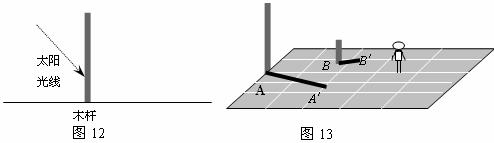
17,(1)一木桿按如圖12所示的方式直立在地面上,請在圖中畫出它在陽光下的影子(用線段CD表示);
(2)如圖13是兩根標桿及它們在燈光下的影子.請在圖中畫出光源的位置(用點P表示);并在圖中畫出人在此光源下的影子(用線段EF表示).
四、(本題共2小題,每小題8分,滿分16分)
18,圖14是某區近期賣出的不同戶型的商品房中隨機抽取1000套進行統計,并根據統計結果繪出如圖所示的統計圖,請結合統計圖提供的信息,解答下列問題:
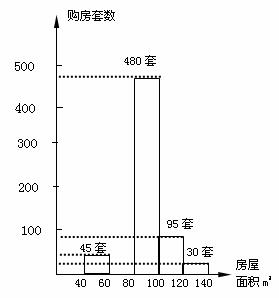
(1)賣出面積為60~80平方米的商品房多少套?并補全統計圖;
(2)請寫出該組數據的中位數所在的范圍;
(3)求面積在什么范圍內的住房賣出最多?約占全部賣出住房的百分之幾?
五.(本題共2小題,每小題10分,滿分20分)
19, 如圖15,某學校九年級數學興趣小組組織一次數學活動.在一座有三道環形路的數字迷宮的每個進口處都標記著一個數,要求進入者把自己當做數“

(1)小軍能進入迷宮中心的概率是多少?請畫出樹狀圖進行說明.
(2)小組兩位組員小張和小李商量做一個小游戲,以猜測小軍進迷宮的結果比勝負.游戲規則規完:小軍如果能進入迷宮中心,小張和小李各得1分;小軍如果不能進入迷宮中心,則他在最后一個進口處所得乘積是奇數時,小張得3分,所得乘積是偶數時,小李得3分,你認為這個游戲公平嗎?如果公平,請說明理由;如果不公平,請在第二道環進口處的兩個數中改變其中一個數使游戲公平.
(3)在(2)的游戲規則下,讓小軍從最外環進口任意進入10次,最終小張和小李的總得分之和不超過28分,請問小軍至少幾次進入迷宮中心?
20, 如圖16,在ㄓABC中,以AB為直徑的⊙O與AC相交于點D,已知AB=10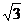 ,CD=5,∠BOD=600
,CD=5,∠BOD=600
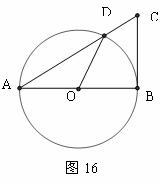
(1)求證:BC是⊙O的切線。
(2)求ㄓABC與⊙O重合部分的面積。
六.(本題滿分12分)
21,如圖17是按一定規律排列的方程組集合和它解的集合的對應關系圖,若方程組處左至右依次記作方程組1、方程組2、方程組3、……方程組n.
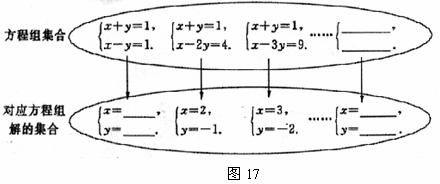
(1)將方程組1的解填入圖中;
(2)請依據方程組和它的解變化的規律,將方程組n和它的解直接填入集合圖中;
(3)若方程組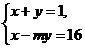 的解是
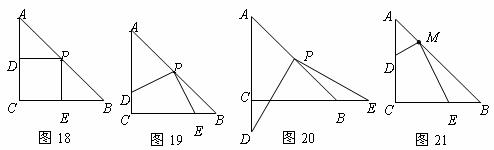
的解是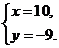 求m的值,并判斷該方程組是否符合(2)中的規律?
求m的值,并判斷該方程組是否符合(2)中的規律?
七.(本題滿分12分)
22,操作:在△ABC中,AC=BC=2,∠C=90°,將一塊等腰直角三角板的直角頂點放在斜邊AB的中點P處,將三角板繞點P旋轉,三角板的兩直角邊分別交射線AC、CB于D、E兩點.如圖18,19,20是旋轉三角板得到的圖形中的3種情況.
探究:(1)三角板繞點P旋轉,通過觀察或測量,猜想線段PD和PE之間有什么數量關系?并結合圖19加以證明.
(2)三角板繞點P旋轉,△PBE是否能成為等腰三角形?若能,寫出△PBE的腰長;若不能,請說明理由.
(3)若將三角板的直角頂點放在斜邊AB上的M處,且AM∶MB=1∶3,和前面一樣操作,試問線段MD和ME之間有什么數量關系?并結合圖21加以證明.
八.(本題滿分14分)
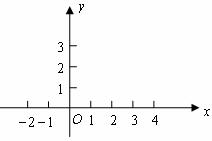
23,已知拋物線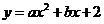 與
與 軸相交于點
軸相交于點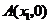 ,
,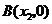
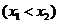 ,且
,且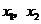 是方程
是方程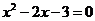 的兩個實數根,點
的兩個實數根,點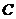 為拋物線與
為拋物線與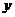 軸的交點.
軸的交點.
(1)求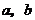 的值;
的值;
(2)分別求出直線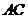 和
和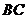 的解析式;
的解析式;
(3)若動直線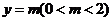 與線段
與線段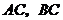 分別相交于
分別相交于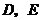 兩點,則在
兩點,則在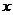 軸上是否存在點
軸上是否存在點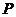 ,使得
,使得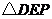 是等腰直角三角形?若存在,求出點
是等腰直角三角形?若存在,求出點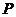 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com