
2008年啟東中學(xué)中考模擬考試
數(shù)學(xué)試卷(十四)
本試卷分第Ⅰ卷(選擇題)和第Ⅱ卷兩部分
第Ⅰ卷(選擇題,共32分)
一、選擇題(本題共10小題;第1~8題每小題3分,第9~10題每小題4分,共32分)
1.要使二次根式 有意義,
有意義,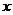 應(yīng)滿足的條件是
應(yīng)滿足的條件是
A.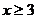 B.
B. C.
C.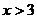 D.
D.
2.規(guī)定一種新的運(yùn)算“*”:對(duì)于任意實(shí)數(shù)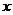 ,
,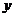 ,滿足
,滿足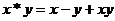 。如
。如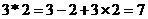 ,則
,則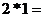
A.4 B.3 C.2 D.1
3.三峽工程是世界防洪效益最為顯著的水利工程,它能有效控制長江上游洪水,增強(qiáng)長江中下游抗洪能力,據(jù)相關(guān)報(bào)道三峽水庫的防洪庫容為
A.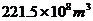 B.
B.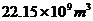
C.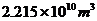 D.
D.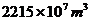
4.足球場(chǎng)平面示意圖如圖1所示,它是軸對(duì)稱圖形,其對(duì)稱軸條數(shù)為
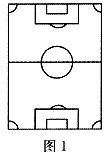
A.1條 B.2條
C.3條 D.4條
5.下列計(jì)算正確的是
A.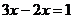 B.
B.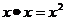
C.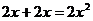 D.
D.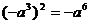
6.圖
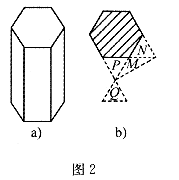
A.P區(qū)域 B.Q區(qū)域
C.M區(qū)域 D.N區(qū)域
7.正比例函數(shù)與反比例函數(shù)的圖像都經(jīng)過點(diǎn)(1,4),在第一象限內(nèi)正比例函數(shù)的圖像在反比例函數(shù)的圖像上方,那么自變量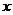 的取值范圍是
的取值范圍是
A.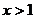 B.
B.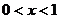 C.
C. D.
D.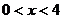
8.銳角三角形的三個(gè)內(nèi)角是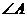 ,
,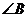 ,
, .如果
.如果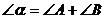 ,
,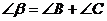 ,
,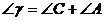 ,那么
,那么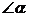 ,
,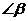 ,
,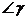 這三個(gè)角中
這三個(gè)角中
A.沒有銳角 B.有1個(gè)銳角 C.有2個(gè)銳角 D.有3個(gè)銳角
9.圖3表示一個(gè)由相同小立方塊搭成的幾何體的俯視圖,小正方形中的數(shù)字表示該位置
上小立方塊的個(gè)數(shù),則該幾何體的主視圖為

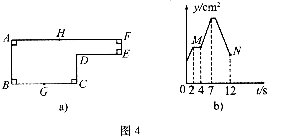
10.已知:如圖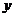 (cm2)關(guān)于運(yùn)動(dòng)時(shí)間
(cm2)關(guān)于運(yùn)動(dòng)時(shí)間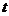 (s)的函數(shù)圖像如圖4b,若AB=
(s)的函數(shù)圖像如圖4b,若AB=
A.1個(gè) B.2個(gè) C.3個(gè) D.4個(gè)
第Ⅱ卷(共118分)
二、填空題(本大題共8小題,每小題3分,共24分,把答案填寫在題中的橫線上.)
11.在函數(shù)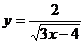 中,自變量
中,自變量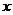 的取值范圍是 .
的取值范圍是 .
12.方程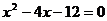 的解是 .
的解是 .
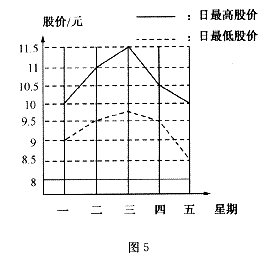
13.如圖5是某只股票從星期一至星期五每天的最高股價(jià)與最低股價(jià)的折線統(tǒng)計(jì)圖,則這五天中最高股價(jià)與最低股價(jià)之差最大的一天是星期 .
14.如圖6,半圓的直徑AB=10,P為AB上一點(diǎn),點(diǎn)C,D為半圓的三等分點(diǎn),則陰影部分的面積等于 .

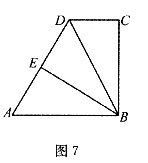
15.如圖7,在梯形ABCD中,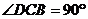 .AB∥CD,
.AB∥CD,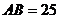 .
.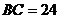 .將該梯形折疊,點(diǎn)A恰好與點(diǎn)D重合,BE為折痕,那么AD的長度為 .
.將該梯形折疊,點(diǎn)A恰好與點(diǎn)D重合,BE為折痕,那么AD的長度為 .
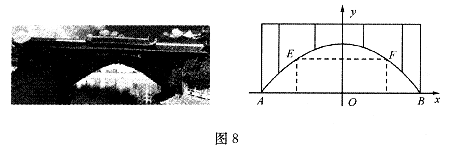
16.廊橋是我國古老的文化遺產(chǎn).如圖8,是某座拋物線型的廊橋示意圖,已知拋物線的函數(shù)表達(dá)式為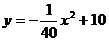 ,為保護(hù)廊橋的安全,在該拋物線上距水面AB高為
,為保護(hù)廊橋的安全,在該拋物線上距水面AB高為
17.如圖9,O為矩形ABCD的中心,將直角三角板的直角頂點(diǎn)與O點(diǎn)重合,轉(zhuǎn)動(dòng)三角板使兩直角邊始終與BC、AB相交,交點(diǎn)分別為M、N.如果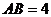 ,
,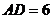 ,
,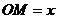 ,
,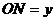 ,則
,則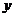 與
與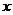 的關(guān)系是 .
的關(guān)系是 .
18.如圖10,在由24個(gè)邊長都為1的小正三角形的網(wǎng)格中,點(diǎn)P是正六邊形的一個(gè)頂點(diǎn),以點(diǎn)P為直角頂點(diǎn)作格點(diǎn)直角三角形(即頂點(diǎn)均在格點(diǎn)上的三角形),請(qǐng)你寫出所有可能的直角三角形斜邊的長 。

三、解答題(本大題共10小題,滿分94分.解答應(yīng)寫出必要的文字說明、證明過程或推演步驟)
19.(本小題滿分6分)計(jì)算或化簡:
(1)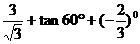
(2)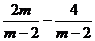
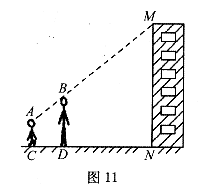
20.(本小題滿分9分)亮亮和穎穎住在同一幢住宅樓,兩人準(zhǔn)備用測(cè)量影子的方法測(cè)算其樓高,但恰逢陰天,于是兩人商定改用下面方法:如圖11,亮亮蹲在地上,穎穎站在亮亮和樓之間,兩人適當(dāng)調(diào)整自己的位置,當(dāng)樓的頂部M,穎穎的頭頂B及亮亮的眼睛A恰在一條直線上時(shí),兩人分別標(biāo)定自己的位置C、D.然后測(cè)出兩人之間的距離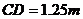 ,穎穎與樓之間的距離
,穎穎與樓之間的距離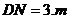 (C、D、N在一條直線上),穎穎的身高
(C、D、N在一條直線上),穎穎的身高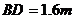 ,亮亮蹲在地上觀測(cè)時(shí)眼睛到地面的距離
,亮亮蹲在地上觀測(cè)時(shí)眼睛到地面的距離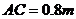 。你能根據(jù)以上測(cè)量數(shù)據(jù)幫助他們求出住宅樓的高度嗎?
。你能根據(jù)以上測(cè)量數(shù)據(jù)幫助他們求出住宅樓的高度嗎?
21.(本小題滿分8分)姚明是我國著名的籃球運(yùn)動(dòng)員,他在這個(gè)賽季NBA常規(guī)賽中表現(xiàn)非常優(yōu)異.下面是他在本賽季中,分別與“超音速”隊(duì)和“快船”隊(duì)各四場(chǎng)比賽中的技術(shù)統(tǒng)計(jì).
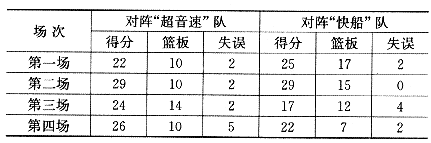
(1)請(qǐng)分別計(jì)算姚明在對(duì)陣“超音速”和“快船”兩隊(duì)的各四場(chǎng)比賽中,平均每場(chǎng)得多少分?
(2)請(qǐng)你從得分的角度分析,姚明在與“超音速”隊(duì)和“快船”隊(duì)的比賽中,對(duì)陣哪一個(gè)隊(duì)的發(fā)揮更穩(wěn)定?
(3)如果規(guī)定“綜合得分”=平均每場(chǎng)得分×1+平均每場(chǎng)籃板× 1.5+平均每場(chǎng)失誤×(一1.5),且綜合得分越高表現(xiàn)越好,那么請(qǐng)你利用這種評(píng)價(jià)方法,來比較姚明在分別與“超音速”隊(duì)和“快船”隊(duì)的四場(chǎng)比賽中,對(duì)陣哪一個(gè)隊(duì)表現(xiàn)得更好?
22.(本題8分)某校團(tuán)委準(zhǔn)備舉辦學(xué)生繪畫展覽,為美化畫面,在長為
23.(本題8分)小明在復(fù)習(xí)數(shù)學(xué)知識(shí)時(shí),針對(duì)“求一元二次方程的解”,整理了以下的幾種方法,請(qǐng)你按有關(guān)內(nèi)容補(bǔ)充完整:

方法一:選擇合適的一種方法(公式法、配方法、分解因式法)求解
解方程: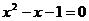
解:
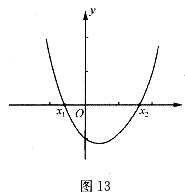
方法二:利用二次函數(shù)圖像與坐標(biāo)軸的交點(diǎn)求解如圖13所示,把方程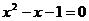 的解看成是二次函數(shù)
的解看成是二次函數(shù)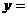 的圖像與
的圖像與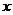 軸交點(diǎn)的橫坐標(biāo),即
軸交點(diǎn)的橫坐標(biāo),即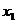 ,
,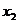 就是方程的解.
就是方程的解.
方法三:利用兩個(gè)函數(shù)圖像的交點(diǎn)求解
(1)把方程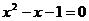 的解看成是一個(gè)二次函數(shù)
的解看成是一個(gè)二次函數(shù)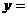 的圖像與一個(gè)一次函數(shù)
的圖像與一個(gè)一次函數(shù)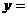 圖像交點(diǎn)的橫坐標(biāo);
圖像交點(diǎn)的橫坐標(biāo);
(2)畫出這兩個(gè)函數(shù)的圖像,用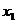 ,
,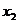 在
在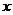 軸上標(biāo)出方程的解.
軸上標(biāo)出方程的解.
24.(本題滿分10分)如圖14,在平面直角坐標(biāo)系中,以坐標(biāo)原點(diǎn)O為圓心,2為半徑畫⊙O,P是⊙O上一動(dòng)點(diǎn),且P在第一象限內(nèi),過點(diǎn)P作⊙O的切線與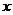 軸相交于點(diǎn)A,與
軸相交于點(diǎn)A,與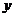 軸相交于點(diǎn)B.
軸相交于點(diǎn)B.
(1)點(diǎn)P在運(yùn)動(dòng)時(shí),線段AB的長度也在發(fā)生變化,請(qǐng)寫出線段AB長度的最小值,并說明理由.
(2)在⊙O上是否存在一點(diǎn)Q,使得以Q,O,A,P為頂點(diǎn)的四邊形是平行四邊形?若存在,請(qǐng)求出Q點(diǎn)的坐標(biāo);若不存在,請(qǐng)說明理由.
25.(本題10分)在課外活動(dòng)時(shí)間,小王、小麗、小華做“互相踢踺子”游戲,踺子從一人傳到另一人就記為踢一次.
(1)若從小麗開始,經(jīng)過兩次踢踺后,踺子踢到小華處的概率是多少?(用樹狀圖或列表法說明)
(2)若經(jīng)過三次踢踺后,踺子踢到小王處的可能性最小,應(yīng)確定從誰開始踢,并說明理由.

26.(本題l2分)某校九年級(jí)三班為開展“迎2008年北京奧運(yùn)會(huì)”的主題班會(huì)活動(dòng),派了小林和小明兩位同學(xué)去學(xué)校附近的超市購買鋼筆作為獎(jiǎng)品.已知該超市的錦江牌鋼筆每支8元,紅梅牌鋼筆每支4.8元,他們要購買這兩種筆共40支.
(1)如果他們兩人一共帶了240元,全部用于購買獎(jiǎng)品,那么能買這兩種筆各多少支?
(2)小林和小明根據(jù)主題班會(huì)活動(dòng)的設(shè)獎(jiǎng)情況,決定所購買的錦江牌鋼筆的數(shù)量要少于紅梅牌鋼筆的數(shù)量的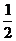 ,但又不少于紅梅牌鋼筆的數(shù)量的
,但又不少于紅梅牌鋼筆的數(shù)量的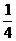 .如果他們買了錦江牌鋼筆
.如果他們買了錦江牌鋼筆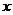 支,買這兩種筆共花了
支,買這兩種筆共花了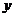 元.
元.
①請(qǐng)寫出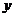 (元)關(guān)于
(元)關(guān)于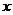 (支)的函數(shù)關(guān)系式,并求出自變量
(支)的函數(shù)關(guān)系式,并求出自變量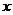 的取值范圍.
的取值范圍.
②請(qǐng)幫他們計(jì)算一下,這兩種筆各購買多少支時(shí),所花的錢最少,此時(shí)花了多少元?
27.(本題10分)在圖16~20中,正方形ABCD的邊長為a,等腰直角三角形FAE的斜邊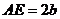 ,且邊AD和AE在同一直線上.
,且邊AD和AE在同一直線上.
操作示例:當(dāng)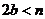 時(shí),如圖16,在BA上選取點(diǎn)G,使
時(shí),如圖16,在BA上選取點(diǎn)G,使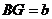 ,連接FG和CG,裁掉△FAG和△CGB并分別拼接到△FEH和△CHD的位置構(gòu)成四邊形FGCH.
,連接FG和CG,裁掉△FAG和△CGB并分別拼接到△FEH和△CHD的位置構(gòu)成四邊形FGCH.
思考發(fā)現(xiàn):小明在操作后發(fā)現(xiàn):該剪拼方法就是先將△FAG繞點(diǎn)F逆時(shí)針旋轉(zhuǎn)90º到△FEH的位置,易知EH與AD在同一直線上.連接CH,由剪拼方法可得 ,故△CHD
≌△CGB,從而又可將△CGB繞點(diǎn)C順時(shí)針旋轉(zhuǎn)90º到△CHD的位置.這樣,對(duì)于剪拼得到的四邊形FGCH(如圖16),過點(diǎn)F作FM上AE于點(diǎn)M(圖略),利用SAS公理可判斷△HFM≌△CHD,易得FH=HC=GC=FG,
,故△CHD
≌△CGB,從而又可將△CGB繞點(diǎn)C順時(shí)針旋轉(zhuǎn)90º到△CHD的位置.這樣,對(duì)于剪拼得到的四邊形FGCH(如圖16),過點(diǎn)F作FM上AE于點(diǎn)M(圖略),利用SAS公理可判斷△HFM≌△CHD,易得FH=HC=GC=FG,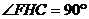 .進(jìn)而根據(jù)正方形的判定方法,可以判斷出四邊形FGCH是正方形.
.進(jìn)而根據(jù)正方形的判定方法,可以判斷出四邊形FGCH是正方形.
實(shí)踐探究:
(1)正方形FGCH的面積是 ;(用含a,b的式子表示)
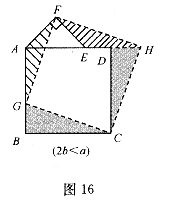
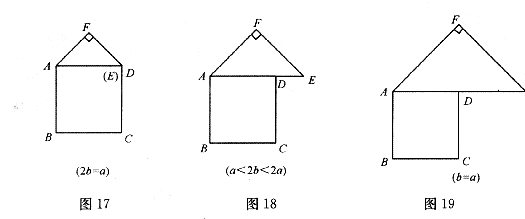
(2)類比圖16的剪拼方法,請(qǐng)你就圖17一圖19的三種情形分別畫出剪拼成一個(gè)新正方形的示意圖.
聯(lián)想拓展:小明通過探究后發(fā)現(xiàn):當(dāng)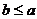 時(shí),此類圖形者能剪拼成正方形,且所選取的點(diǎn)G的位置在BA方向上隨著b的增大不斷上移.當(dāng)
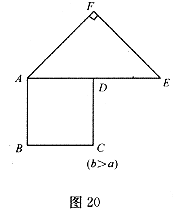
時(shí),此類圖形者能剪拼成正方形,且所選取的點(diǎn)G的位置在BA方向上隨著b的增大不斷上移.當(dāng)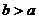 時(shí),如圖20的圖形能否剪拼成一個(gè)正方形?若能請(qǐng)你在圖中畫出剪拼的示意圖;若不能,簡要說明理由.
時(shí),如圖20的圖形能否剪拼成一個(gè)正方形?若能請(qǐng)你在圖中畫出剪拼的示意圖;若不能,簡要說明理由.
28.(本題13分)如圖21,在平面直角坐標(biāo)系中,已知點(diǎn)A(0,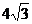 ),點(diǎn)B在z正半軸上,且
),點(diǎn)B在z正半軸上,且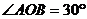 .動(dòng)點(diǎn)P在線段AB上從點(diǎn)A向點(diǎn)8以每秒
.動(dòng)點(diǎn)P在線段AB上從點(diǎn)A向點(diǎn)8以每秒 個(gè)單位的速度運(yùn)動(dòng),設(shè)運(yùn)動(dòng)時(shí)間為
個(gè)單位的速度運(yùn)動(dòng),設(shè)運(yùn)動(dòng)時(shí)間為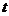 秒.在z軸上取兩點(diǎn)M, N作等邊△PMN.
秒.在z軸上取兩點(diǎn)M, N作等邊△PMN.
(1)求直線AB的解析式.
(2)求等邊△PMN的邊長(用t的代數(shù)式表示),并求出當(dāng)?shù)冗叀鱌MN的頂點(diǎn)M運(yùn)動(dòng)到與原點(diǎn)。重合時(shí)t的值.
(3)如果取OB的中點(diǎn)D,以0D為邊在Rt△A()B內(nèi)部作如圖22所示的矩形ODCE,點(diǎn)C在線段AB上.設(shè)等邊△PMN和矩形ODCE重疊部分的面積為S,請(qǐng)求出當(dāng)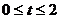 秒時(shí)S與
秒時(shí)S與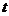 的函數(shù)關(guān)系式,并求出S的最大值。
的函數(shù)關(guān)系式,并求出S的最大值。

百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com