|
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
12.已知O是平面上的一個定點,A、B、C是平面上不共線的三個點,動點P滿足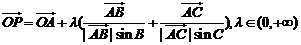 ,則動點P的軌跡一定通過△ABC的( ) ,則動點P的軌跡一定通過△ABC的( ) 試題詳情
A.垂心 B.重心 C.外心 D.內心 試題詳情
二、填空題:(本大題共4小題,每小題4分,共16分,請把答案填在答題卡上。)
試題詳情
試題詳情
試題詳情
16.給出下列命題: 試題詳情
試題詳情
試題詳情
C.底面是等邊三角形,側面都是等腰三角形的三棱錐是正三棱錐。 試題詳情
試題詳情
其中正確的命題是
(把所有正確的命題的選項都填上) 試題詳情
三、解答題:(本大題共6小題,共74分。解答應寫出文字說明,證明過程或演算步驟。) 17.(本小題滿分12分) 試題詳情
試題詳情
(Ⅰ)求角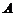 的大小; 的大小; 試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
18.(本小題滿分12分) 試題詳情
試題詳情
(Ⅰ)求在5月13日恰有1支隊伍抵達災區的概率; 試題詳情
(Ⅱ)求在5月13日抵達災區的隊伍數為多少時概率最大。 試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
19.(本小題滿分12分) 試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
20.(本小題滿分12分) 試題詳情
如圖,已知正三棱柱ABC-A1B1C1的側棱長和底面邊長均為1, 試題詳情
M是底面BC邊上的中點,N是側棱CC1上的點,且CN=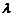 NC1. NC1. 試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
21.(本小題滿分12分) 試題詳情
試題詳情
試題詳情
試題詳情
(Ⅰ)求 的解析式; 的解析式; 試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
(Ⅱ)試根據(Ⅰ)中的結論猜測:橢圓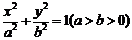 的“左特征點”M是一個怎樣的點?并證明你的結論. 的“左特征點”M是一個怎樣的點?并證明你的結論. 2009屆師大附中、鷹潭一中高三聯考 試題詳情
一、選擇題 1--5 ADACB 6--10 ABACD 11―12 CB 二、填空題 13.8 14.7 15.12 16.AB 三、解答題 17.解:(Ⅰ)  , ,  , ,
 .…………………………(4分) .…………………………(4分)
  , ,  .………………………(6分) .………………………(6分)
(Ⅱ)由余弦定理 ,得 ,得  .………(8分) .………(8分)  , ,  . .
  所以 所以 的最小值為 的最小值為 ,當且僅當 ,當且僅當 時取等號.………………(12分) 時取等號.………………(12分)
 18.(Ⅰ)解法一:依據題意,因為隊伍從水路或陸路抵達災區的概率相等,則將“隊伍從水路或陸路抵達災區”視為同一個事件. 記“隊伍從水路或陸路抵達災區”為事件C,且B、C相互獨立,而且 18.(Ⅰ)解法一:依據題意,因為隊伍從水路或陸路抵達災區的概率相等,則將“隊伍從水路或陸路抵達災區”視為同一個事件. 記“隊伍從水路或陸路抵達災區”為事件C,且B、C相互獨立,而且 .……………………………(2分) .……………………………(2分)
在5月13日恰有1支隊伍抵達災區的概率是  .……………………(6分) .……………………(6分)
解法二:在5月13日恰有1支隊伍抵達災區的概率是  .…………(6分) .…………(6分)
(Ⅱ)依據題意,因為隊伍從水路或陸路抵達災區的概率相等,則將“隊伍從水路或陸路抵達災區”視為同一個事件. 記“隊伍從水路或陸路抵達災區”為事件C,且B、C相互獨立,而且 . . 設5月13日抵達災區的隊伍數為 ,則 ,則 =0、1、2、3、4. ……………………(7分) =0、1、2、3、4. ……………………(7分) 由已知有: ; ;  ; ;
 ; ;
 ; ;
 . .
答:在5月13日抵達災區的隊伍數為2時概率最大……………………(12分) 19. (I)由已知a2-a1=-2, a3-a2=-1, -1-(-2)=1 ∴an+1-an=(a2-a1)+(n-1)?1=n-3 n≥2時,an=( an-an-1)+( an-1-an-2)+…+( a3-a2)+( a2-a1)+ a1 =(n-4)+(n-5) +…+(-1)+(-2)+6 = n=1也合適. ∴an= (n∈N*) ……………………3分 (n∈N*) ……………………3分 又b1-2=4、b2-2=2 .而 ∴bn-2=(b1-2)?( ∴bn-2=(b1-2)?( )n-1即bn=2+8?( )n-1即bn=2+8?( )n……(6分) )n……(6分) ∴數列{an}、{bn}的通項公式為:an= ,bn=2+( ,bn=2+( )n-3 )n-3  (II)設 (II)設
  當k≥4時 當k≥4時 為k的增函數,-8?( 為k的增函數,-8?( )k也為k的增函數,而f(4)= )k也為k的增函數,而f(4)= 
 ∴當k≥4時ak-bk≥ ∴當k≥4時ak-bk≥ ………………10分 ………………10分
又f(1)=f(2)=f(3)=0 ∴不存在k, 使f(k)∈(0, )…………12分 )…………12分 20解法1:(Ⅰ)因為M是底面BC邊上的中點,且AB=AC,所以AM BC, BC,  在正三棱柱ABC-A1B1C1中, 在正三棱柱ABC-A1B1C1中, 底面 底面 , ,  AM AM  又 又 .所以AM .所以AM 平面 平面  . .
(或:連結 , , 又 又 , , .)…………(5分) .)…………(5分) (II)因為AM 平面 平面  且 M M 平面 平面  ,NM ,NM 平面 平面  ∴AM  M, AM M, AM NM, NM, ∴  MN為二面角 MN為二面角 ―AM―N的平面角. …………(7分) ―AM―N的平面角. …………(7分) ∴ ,設C1N= ,設C1N= ,則CN=1- ,則CN=1- 又 M= M=  ,MN= ,MN= , ,  連 連 N,得 N,得 N= N= , ,
在  MN中,由余弦定理得 MN中,由余弦定理得  , …(10分) , …(10分)
得 = = .故 .故 =2. … (12分) =2. … (12分) 解法2:(Ⅰ)建立如圖所示的空間直角坐標系,則 (0,0,1),M(0, (0,0,1),M(0, ,0), ,0), C(0,1,0), A ( ),設N (0,1,a) ,所以, ),設N (0,1,a) ,所以,  , , , ,
因為 所以 所以 ,同法可得 ,同法可得 .又 .又 故AM 故AM 面BC 面BC  . . (II)由(Ⅰ)知? ?為二面角 ?為二面角 ―AM―N的平面角,以下同法一. ―AM―N的平面角,以下同法一. 21解(Ⅰ)由已知  ∴ ∴ ∴ ∴ ………………(2分) ………………(2分)
又 且 且 ∴ ∴ (舍去 (舍去 ) ) ∴ …(4分) …(4分) (Ⅱ)令 即 即 的增區間為 的增區間為 、 、 ∵ 在區間 在區間 上是增函數 上是增函數 ∴ 或 或 則 則 或 或 ……(8分) ……(8分) (Ⅲ)令 或 或 ∵ ∴ 在 在 上的最大值為4,最小值為0………………(10分) 上的最大值為4,最小值為0………………(10分) ∴ 、 、 時, 時, ……………(12分) ……………(12分) 22.解 (1)設 為橢圓 為橢圓 的左特征點,橢圓的左焦點為 的左特征點,橢圓的左焦點為 ,可設直線 ,可設直線 的方程為 的方程為 .并將它代入 .并將它代入 得: 得: ,即 ,即 .設 .設 ,則 ,則 ,……(3分) ,……(3分) ∵ 被 被 軸平分,∴ 軸平分,∴ .即 .即 . . 即 ,∴ ,∴ .……………(5分) .……………(5分) 于是 . . ∵ ,即 ,即 .………………(7分) .………………(7分) (2)對于橢圓 .于是猜想:橢圓 .于是猜想:橢圓 的“左特征點”是橢圓的左準線與 的“左特征點”是橢圓的左準線與 軸的交點. ………………(9分) 軸的交點. ………………(9分)  證明:設橢圓的左準線 證明:設橢圓的左準線 與 與 軸相交于M點,過A,B分別作 軸相交于M點,過A,B分別作 的垂線,垂足分別為C,D. 的垂線,垂足分別為C,D.
據橢圓第二定義: ∵ ∵  于是 即 即 .∴ .∴ ,又 ,又 均為銳角,∴ 均為銳角,∴ ,∴ ,∴ . . ∴ 的平分線.故M為橢圓的“左特征點”. ………(14分) 的平分線.故M為橢圓的“左特征點”. ………(14分)
主站蜘蛛池模板:
玖玖精品|
久久精品国产一区
|
日韩中文字幕一区二区
|
亚洲成人毛片
|
久久久久久亚洲
|
91人人插
|
成人免费在线看片
|
蜜臀va亚洲va欧美va天堂
|
久久国产精品一区二区
|
色视频免费
|
极品美女一区二区三区
|
色综合久久88色综合天天
|
97香蕉久久国产超碰青草软件
|
日韩专区在线播放
|
免费在线成人av
|
国产精品成人在线观看
|
欧美一区二区在线视频
|
中文字幕一区二区在线观看
|
自拍偷拍小视频
|
成人免费视频一区二区
|
亚洲毛片网站
|
欧美日韩亚洲国产综合
|
久久99精品久久久久久按摩秒播
|
精品在线不卡
|
在线欧美色|
国产一区二区在线免费观看
|
免费看91|
av网站免费在线观看
|
四虎永久在线
|
欧美色爽
|
欧美日韩一区二区三区在线观看
|
一级毛片在线视频
|
中文字幕乱码亚洲精品一区
|
热久久免费视频
|
久草院线
|
xxxx欧美
|
国产精品自拍av
|
日韩视频免费
|
黄av免费
|
久久精品123|
亚洲成人伦理
|
| 



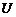 ={1,2,3,4,5,6},集合
={1,2,3,4,5,6},集合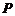 ={1,2,3,4},
={1,2,3,4},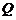 ={3,4,5,6},則
={3,4,5,6},則 =( )
=( )
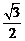 D.1
D.1
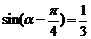 ,則
,則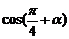 的值等于( )
的值等于( )
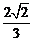 B.-
B.-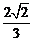 C.
C.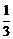 D.-
D.-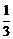

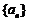 是等差數列,且
是等差數列,且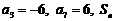 是數列
是數列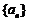 的前n項和,則( )
的前n項和,則( )
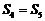 B.
B.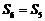 C.
C. D.
D.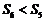

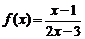 的反函數是
的反函數是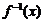 ,則
,則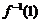 =( )
=( )

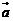 與
與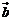 的夾角為
的夾角為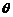 ,定義
,定義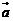 與
與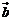 的“向量積”:
的“向量積”: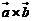 是一個向量,它的模
是一個向量,它的模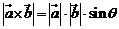 ,若
,若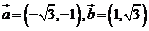 ,則
,則 ( )
( )
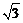 B.2 C.
B.2 C.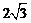 D.4
D.4
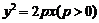 的焦點作直線交拋物線于
的焦點作直線交拋物線于 ,
,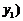 、
、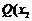 ,
,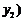 兩點,若
兩點,若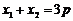 ,則
,則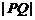 等于( )
等于( )

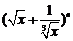 的各項系數之和大于
的各項系數之和大于 ,小于
,小于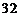 ,則展開式中系數最大的項是( )
,則展開式中系數最大的項是( ) 
 A.
A.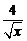 B.
B.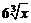 C.
C.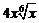 D.
D.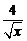 或
或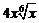



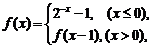 若方程
若方程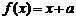 有且只有兩個不相等的實數根,則實數
有且只有兩個不相等的實數根,則實數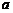 的取值范圍為( )
的取值范圍為( )
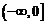 B.
B.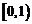 C.
C.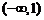 D.
D.