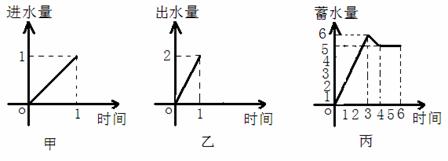
n=5 s=0 WHILE s<14 s=s+n n=n-1 WAND PRINT n END A、-1
B、0 C、1 D、2
試題詳情
二、填空題:(本大題共6個小題,每小題5分,共30分,把答案寫在橫線上). 9、某市高三數學抽樣考試中,對90分以上(含90分)的成績進行統計,其頻率分布圖
試題詳情
如圖所示,若130-140分數段的人數為90人,則90-100分數段的人數為 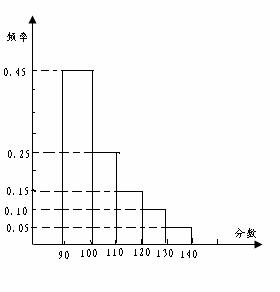 試題詳情
10.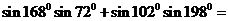 .
. 試題詳情
11.已知i, j為互相垂直的單位向量,a = i ? 2j, b = i + λj,且a與b的夾角為銳角,則實數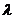 的取值范圍是 . 的取值范圍是 . 試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
(3)函數 是周期函數;
(4)函數 是周期函數;
(4)函數 是增函數. 是增函數. 試題詳情
14.在平面直角坐標系中,已知曲線c: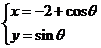 ,( ,(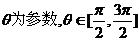 ) ) 則曲線c關于y=x對稱的曲線方程是
試題詳情
三、解答題:本大題共6小題,滿分74分,解答應寫出文字說明,證明過程或演算步驟. 15.(本題滿分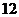 分) 分) 試題詳情
已知 , , 試題詳情
(Ⅰ)求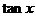 的值;(Ⅱ)求 的值;(Ⅱ)求 的值. 的值. 試題詳情
16.(本題滿分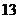 分) 分) 試題詳情
試題詳情
(Ⅰ)求隨機變量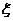 的最大值,并求事件“ 的最大值,并求事件“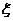 取得最大值”的概率; 取得最大值”的概率; 試題詳情
(Ⅱ)求隨機變量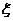 的分布列和數學期望. 的分布列和數學期望. 試題詳情
17.(本題滿分 分) 分) 試題詳情
試題詳情
(Ⅱ) 求二面角 的大小; 的大小; 試題詳情
(Ⅲ)求點 到平面 到平面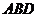 的距離. 的距離. 試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
(Ⅲ)設直線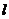 與橢圓 與橢圓 的兩條準線分別交于 的兩條準線分別交于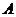 、 、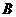 兩點,點 兩點,點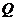 為線段 為線段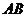 上的動點,求點 上的動點,求點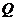 到 到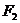 的距離與到橢圓 的距離與到橢圓 右準線的距離之比的最小值,并求取得最小值時點 右準線的距離之比的最小值,并求取得最小值時點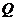 的坐標. 的坐標. 試題詳情
19.(本題滿分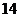 分) 分) 試題詳情
已知數列 滿足: 滿足: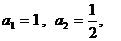 且 且 試題詳情
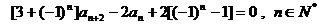 . .
試題詳情
試題詳情
試題詳情
20.(本題滿分 分) 分) 試題詳情
試題詳情
(Ⅰ)設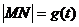 ,試求函數 ,試求函數 的表達式; 的表達式; 試題詳情
試題詳情
(Ⅲ)在(Ⅰ)的條件下,若對任意的正整數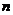 ,在區間 ,在區間 內總存在 內總存在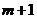 個實數 個實數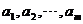 , ,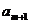 ,使得不等式 ,使得不等式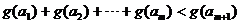 成立,求 成立,求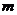 的最大值. 的最大值. 試題詳情
一、選擇題: 1. 答案:C.  {x | x≥0},故選C. {x | x≥0},故選C. 2.C 3. (理)對于 中,當n=6時,有 中,當n=6時,有 所以第25項是7.選C. 所以第25項是7.選C. 4.D 5.A. ∵ = , , ∴根據題意作出函數圖象即得.選A. 6. 答案:D.當x=1時,y=m ,由圖形易知m<0, 又函數是減函數,所以0<n<1,故選D. 7.A 8.C 二、填空題: 9.810 10.答案: . .   
11. 答案: . . 
12. 13. (2)、(3) 14. 15.(本題滿分 分) 分) 已知 , , (Ⅰ)求 的值; 的值; (Ⅱ)求 的值. 的值. 解:(Ⅰ)由 , ,  ,
………………………2分 ,
………………………2分
 .
…………………5分 .
…………………5分 (Ⅱ) 原式=  
 …………………10分
…………………10分

  .
…………………12分 .
…………………12分
16.(本題滿分 分) 分) 在一個盒子中,放有標號分別為 , , , , 的三張卡片,現從這個盒子中,有放回地先后抽得兩張卡片的標號分別為 的三張卡片,現從這個盒子中,有放回地先后抽得兩張卡片的標號分別為 、 、 ,記 ,記 . . (Ⅰ)求隨機變量 的最大值,并求事件“ 的最大值,并求事件“ 取得最大值”的概率; 取得最大值”的概率; (Ⅱ)求隨機變量 的分布列和數學期望. 的分布列和數學期望. 解:(Ⅰ) 、 、 可能的取值為 可能的取值為 、 、 、 、 , ,  , , , ,  ,且當 ,且當 或 或 時, 時, .
……………3分 .
……………3分
因此,隨機變量 的最大值為 的最大值為 . .  有放回抽兩張卡片的所有情況有 有放回抽兩張卡片的所有情況有 種, 種,
 . .
答:隨機變量 的最大值為 的最大值為 ,事件“ ,事件“ 取得最大值”的概率為 取得最大值”的概率為 . ………5分 . ………5分 (Ⅱ) 的所有取值為 的所有取值為 . .  時,只有 時,只有 這一種情況, 這一種情況,
 時,有 時,有 或 或 或 或 或 或 四種情況, 四種情況,  時,有 時,有 或 或 兩種情況. 兩種情況.
 , , , , .
…………11分 .
…………11分
則隨機變量 的分布列為: 的分布列為: 









因此,數學期望 . ……………………13分 . ……………………13分 17.(本題滿分 分) 分) 如圖,已知正三棱柱 ― ― 的底面邊長是 的底面邊長是 , , 是側棱 是側棱 的中點,直線 的中點,直線 與側面 與側面 所成的角為 所成的角為 . . (Ⅰ)求此正三棱柱的側棱長;(Ⅱ) 求二面角 的大小; 的大小; (Ⅲ)求點 到平面 到平面 的距離. 的距離.  解:(Ⅰ)設正三棱柱 解:(Ⅰ)設正三棱柱 ― ― 的側棱長為 的側棱長為 .取 .取 中點 中點 ,連 ,連 . .
 是正三角形, 是正三角形, . .
又底面 側面 側面 ,且交線為 ,且交線為 . .  側面 側面 . .
連 ,則直線 ,則直線 與側面 與側面 所成的角為 所成的角為 . ……………2分 . ……………2分 在 中, 中, ,解得 ,解得 . …………3分 . …………3分  此正三棱柱的側棱長為 此正三棱柱的側棱長為 .
……………………4分 .
……………………4分
注:也可用向量法求側棱長. (Ⅱ)解法1:過 作 作 于 于 ,連 ,連 , ,  側面 側面   . .
 為二面角 為二面角 的平面角.
……………………………6分 的平面角.
……………………………6分
在 中, 中, ,又 ,又  , ,   . .
又  在 在 中, 中, .
…………………………8分 .
…………………………8分
故二面角 的大小為 的大小為 .
…………………………9分 .
…………………………9分 解法2:(向量法,見后) (Ⅲ)解法1:由(Ⅱ)可知, 平面 平面 , , 平面 平面 平面 平面 ,且交線為 ,且交線為 , , 過 過 作 作 于 于 ,則 ,則 平面 平面 .
…………10分 .
…………10分 在 中, 中, .
…………12分 .
…………12分   為 為 中點, 中點, 點 點 到平面 到平面 的距離為 的距離為 . …………13分 . …………13分
解法2:(思路)取 中點 中點 ,連 ,連 和 和 ,由 ,由  ,易得平面 ,易得平面 平面 平面 ,且交線為 ,且交線為 .過點 .過點 作 作 于 于 ,則 ,則 的長為點 的長為點 到平面 到平面 的距離. 的距離. 解法3:(思路)等體積變換:由 可求. 可求. 解法4:(向量法,見后) 題(Ⅱ)、(Ⅲ)的向量解法:  (Ⅱ)解法2:如圖,建立空間直角坐標系 (Ⅱ)解法2:如圖,建立空間直角坐標系 . .
則 . . 設  為平面 為平面 的法向量. 的法向量. 由 得 得  . .  取 取 …………6分
…………6分
又平面 的一個法向量 的一個法向量 …………7分
…………7分   . …………8分 . …………8分
結合圖形可知,二面角 的大小為 的大小為 .
…………9分 .
…………9分 (Ⅲ)解法4:由(Ⅱ)解法2,  …………10分 …………10分  點 點 到平面 到平面 的距離 的距離  = = .13分 .13分
18. (本小題滿分14分) 一束光線從點 出發,經直線 出發,經直線 上一點 上一點 反射后,恰好穿過點 反射后,恰好穿過點 . . (Ⅰ)求點 關于直線 關于直線 的對稱點 的對稱點 的坐標; 的坐標; (Ⅱ)求以 、 、 為焦點且過點 為焦點且過點 的橢圓 的橢圓 的方程; 的方程; (Ⅲ)設直線 與橢圓 與橢圓 的兩條準線分別交于 的兩條準線分別交于 、 、 兩點,點 兩點,點 為線段 為線段 上的動點,求點 上的動點,求點 到 到 的距離與到橢圓 的距離與到橢圓 右準線的距離之比的最小值,并求取得最小值時點 右準線的距離之比的最小值,并求取得最小值時點 的坐標. 的坐標. 解:(Ⅰ)設 的坐標為 的坐標為 ,則 ,則 且 且 .……2分 .……2分 解得 , 因此,點 , 因此,點  的坐標為 的坐標為 . …………………4分 . …………………4分 (Ⅱ) ,根據橢圓定義, ,根據橢圓定義, 得  ,……………5分 ,……………5分  , , . .
∴所求橢圓方程為 .
………………………………7分 .
………………………………7分 (Ⅲ) , , 橢圓的準線方程為 橢圓的準線方程為 . …………………………8分 . …………………………8分 設點 的坐標為 的坐標為  , , 表示點 表示點 到 到 的距離, 的距離, 表示點 表示點 到橢圓的右準線的距離. 到橢圓的右準線的距離. 則 , , . .  ,
……………………………10分 ,
……………………………10分
令  ,則 ,則 , ,  當 當 , , , ,
 , , . .
∴  在 在 時取得最小值.
………………………………13分 時取得最小值.
………………………………13分 因此, 最小值= 最小值= ,此時點 ,此時點 的坐標為 的坐標為 .…………14分 .…………14分 注: 的最小值還可以用判別式法、換元法等其它方法求得. 的最小值還可以用判別式法、換元法等其它方法求得. 說明:求得的點  即為切點 即為切點 , , 的最小值即為橢圓的離心率. 的最小值即為橢圓的離心率. 19.(本題滿分 分) 分) 已知數列 滿足: 滿足: 且 且 , , . . (Ⅰ)求 , , , , , , 的值及數列 的值及數列 的通項公式; 的通項公式; (Ⅱ)設 ,求數列 ,求數列 的前 的前 項和 項和 ; ; 解:(Ⅰ)經計算 , , , , , , . . 當 為奇數時, 為奇數時, ,即數列 ,即數列 的奇數項成等差數列, 的奇數項成等差數列,  ; ;
當 為偶數, 為偶數, ,即數列 ,即數列 的偶數項成等比數列, 的偶數項成等比數列,  . .
因此,數列 的通項公式為 的通項公式為 . . (Ⅱ)  , ,
 ……(1) ……(1)
 …(2) …(2) (1)、(2)兩式相減, 得
  . .
 . .
20.(本題滿分 分) 分) 已知函數 和點 和點 ,過點 ,過點 作曲線 作曲線 的兩條切線 的兩條切線 、 、 ,切點分別為 ,切點分別為 、 、 . . (Ⅰ)設 ,試求函數 ,試求函數 的表達式; 的表達式; (Ⅱ)是否存在 ,使得 ,使得 、 、 與 與 三點共線.若存在,求出 三點共線.若存在,求出 的值;若不存在,請說明理由. 的值;若不存在,請說明理由. (Ⅲ)在(Ⅰ)的條件下,若對任意的正整數 ,在區間 ,在區間 內總存在 內總存在 個實數 個實數  , , ,使得不等式 ,使得不等式 成立,求 成立,求 的最大值. 的最大值.
解:(Ⅰ)設 、 、 兩點的橫坐標分別為 兩點的橫坐標分別為 、 、 , ,   , ,  切線 切線 的方程為: 的方程為: , ,
又 切線 切線 過點 過點 , ,  有 有 , , 即 , ………………………………………………(1) …… 2分 , ………………………………………………(1) …… 2分 同理,由切線 也過點 也過點 ,得 ,得 .…………(2) .…………(2) 由(1)、(2),可得 是方程 是方程 的兩根, 的兩根,  ………………( * )
……………………… 4分 ………………( * )
……………………… 4分
 
 , , 把( * )式代入,得 , , 因此,函數 的表達式為 的表達式為 . ……………………5分 . ……………………5分 (Ⅱ)當點 、 、 與 與 共線時, 共線時, , ,  = = , , 即 = = ,化簡,得 ,化簡,得 , ,  , , . ………………(3) …………… 7分 . ………………(3) …………… 7分
把(*)式代入(3),解得 . .  存在 存在 ,使得點 ,使得點 、 、 與 與 三點共線,且 三點共線,且  . ……………………9分 . ……………………9分
(Ⅲ)解法 :易知 :易知 在區間 在區間 上為增函數, 上為增函數,    , ,
則 . . 依題意,不等式 對一切的正整數 對一切的正整數 恒成立, …………11分 恒成立, …………11分  , ,
即 對一切的正整數 對一切的正整數
主站蜘蛛池模板:
日韩av电影网
|
久久综合99re88久久爱
|
欧美激情五月
|
特级毛片在线观看
|
色视频免费
|
中文二区
|
精品免费国产一区二区三区
|
夜夜夜久久久
|
亚洲精品1区
|
日韩欧美综合
|
自拍偷拍欧美日韩
|
国产不卡视频一区二区三区
|
亚洲精品一区二区三区在线
|
亚洲视频手机在线观看
|
999国产在线
|
在线观看欧美日韩视频
|
五月天电影网
|
一区二区三区欧美在线
|
天堂久久一区
|
亚洲国产高清高潮精品美女
|
污网站在线看
|
亚洲天堂美女视频
|
国产成人精品高清久久
|
91亚洲精品一区
|
国产在线a视频
|
五月天最新网址
|
精品视频久久久
|
精品国内视频
|
亚洲激情在线播放
|
国产精品一码二码三码在线
|
欧美猛交ⅹxxx乱大交视频
|
国产成人av一区二区
|
麻豆专区一区二区三区四区五区
|
久久久久无码国产精品一区
|
精品国产乱码一区二区三
|
黄色毛片视频网站
|
人人爽日日爽
|
自拍偷拍欧美
|
福利社午夜影院
|
亚州精品成人
|
性培育学校羞耻椅子调教h
另类中文字幕
|
| 
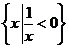 ,則
,則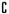 UA=( ).
UA=( ). B.{x | x > 0} C.{x | x≥0} D.
B.{x | x > 0} C.{x | x≥0} D.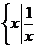 ≥0
≥0
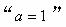 是
是 “函數
“函數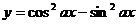 的最小正周期為
的最小正周期為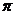 ”的 ( ).
”的 ( ).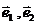 不共線,若
不共線,若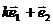 與
與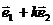 也不共線,則實數k的取值范圍為
也不共線,則實數k的取值范圍為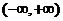 B.
B.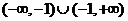
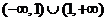 D.
D.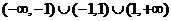
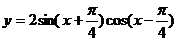 和直線
和直線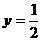 在y軸右側的交點按橫坐標從小到大依次記為P1,P2,P3,…,則|P2P4|等于( ).
在y軸右側的交點按橫坐標從小到大依次記為P1,P2,P3,…,則|P2P4|等于( ).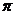 B.2
B.2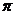 C.3
C.3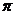 D.4
D.4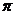
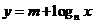 的圖象,其中m,n為常數,
的圖象,其中m,n為常數,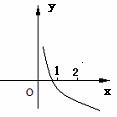
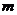 < 0 , n >1
B.
< 0 , n >1
B.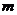 > 0 , n > 1
> 0 , n > 1 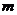 > 0 , 0 < n <1 D.
> 0 , 0 < n <1 D. 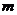 < 0 , 0 < n < 1
< 0 , 0 < n < 1