高考數(shù)學(xué)復(fù)習(xí)易做易錯(cuò)題選
排列組合易錯(cuò)題正誤解析
排列組合問題類型繁多、方法豐富、富于變化，稍不注意，極易出錯(cuò).本文選擇一些在教學(xué)中學(xué)生常見的錯(cuò)誤進(jìn)行正誤解析，以饗讀者.
1沒有理解兩個(gè)基本原理出錯(cuò)
排列組合問題基于兩個(gè)基本計(jì)數(shù)原理，即加法原理和乘法原理，故理解“分類用加、分步用乘”是解決排列組合問題的前提.
例1（1995年上海高考題）從6臺(tái)原裝計(jì)算機(jī)和5臺(tái)組裝計(jì)算機(jī)中任意選取5臺(tái),其中至少有原裝與組裝計(jì)算機(jī)各兩臺(tái),則不同的取法有 種.
誤解：因?yàn)榭梢匀?臺(tái)原裝與3臺(tái)組裝計(jì)算機(jī)或是3臺(tái)原裝與2臺(tái)組裝計(jì)算機(jī)，所以只有2種取法.
錯(cuò)因分析：誤解的原因在于沒有意識(shí)到“選取2臺(tái)原裝與3臺(tái)組裝計(jì)算機(jī)或是3臺(tái)原裝與2臺(tái)組裝計(jì)算機(jī)”是完成任務(wù)的兩“類”辦法，每類辦法中都還有不同的取法.
正解：由分析，完成第一類辦法還可以分成兩步：第一步在原裝計(jì)算機(jī)中任意選取2臺(tái)，有
種方法；第二步是在組裝計(jì)算機(jī)任意選取3臺(tái)，有
種方法，據(jù)乘法原理共有
種方法.同理，完成第二類辦法中有
種方法.據(jù)加法原理完成全部的選取過程共有
種方法.
例2 在一次運(yùn)動(dòng)會(huì)上有四項(xiàng)比賽的冠軍在甲、乙、丙三人中產(chǎn)生，那么不同的奪冠情況共有（ ）種.
（A）
（B）
（C）
（D）
誤解：把四個(gè)冠軍，排在甲、乙、丙三個(gè)位置上，選A.
錯(cuò)因分析：誤解是沒有理解乘法原理的概念，盲目地套用公式.
正解：四項(xiàng)比賽的冠軍依次在甲、乙、丙三人中選取，每項(xiàng)冠軍都有3種選取方法，由乘法原理共有
種.
說明：本題還有同學(xué)這樣誤解，甲乙丙奪冠均有四種情況，由乘法原理得.這是由于沒有考慮到某項(xiàng)冠軍一旦被一人奪得后，其他人就不再有4種奪冠可能.
2判斷不出是排列還是組合出錯(cuò)
在判斷一個(gè)問題是排列還是組合問題時(shí)，主要看元素的組成有沒有順序性，有順序的是排列，無順序的是組合.
例3 有大小形狀相同的3個(gè)紅色小球和5個(gè)白色小球，排成一排，共有多少種不同的排列方法？
誤解：因?yàn)槭?個(gè)小球的全排列，所以共有
種方法.
錯(cuò)因分析：誤解中沒有考慮3個(gè)紅色小球是完全相同的，5個(gè)白色小球也是完全相同的，同色球之間互換位置是同一種排法.
正解：8個(gè)小球排好后對(duì)應(yīng)著8個(gè)位置，題中的排法相當(dāng)于在8個(gè)位置中選出3個(gè)位置給紅球，剩下的位置給白球，由于這3個(gè)紅球完全相同，所以沒有順序，是組合問題.這樣共有：
排法.
3重復(fù)計(jì)算出錯(cuò)
在排列組合中常會(huì)遇到元素分配問題、平均分組問題等，這些問題要注意避免重復(fù)計(jì)數(shù)，產(chǎn)生錯(cuò)誤。
例4（2002年北京文科高考題）5本不同的書全部分給4個(gè)學(xué)生，每個(gè)學(xué)生至少一本，不同的分法種數(shù)為（ ）
（A）480 種 （B）240種 （C）120種 （D）96種
誤解：先從5本書中取4本分給4個(gè)人，有
種方法，剩下的1本書可以給任意一個(gè)人有4種分法，共有
種不同的分法，選A.
錯(cuò)因分析：設(shè)5本書為
、
、
、
、
，四個(gè)人為甲、乙、丙、丁.按照上述分法可能如下的表1和表2：
表1是甲首先分得、乙分得、丙分得、丁分得，最后一本書給甲的情況；表2是甲首先分得、乙分得、丙分得、丁分得，最后一本書給甲的情況.這兩種情況是完全相同的，而在誤解中計(jì)算成了不同的情況。正好重復(fù)了一次.
正解：首先把5本書轉(zhuǎn)化成4本書，然后分給4個(gè)人.第一步：從5本書中任意取出2本捆綁成一本書，有
種方法；第二步：再把4本書分給4個(gè)學(xué)生，有
種方法.由乘法原理，共有
種方法，故選B.
例5 某交通崗共有3人，從周一到周日的七天中，每天安排一人值班，每人至少值2天，其不同的排法共有（ ）種.
（A）5040 （B）1260 （C）210 （D）630
誤解：第一個(gè)人先挑選2天，第二個(gè)人再挑選2天，剩下的3天給第三個(gè)人，這三個(gè)人再進(jìn)行全排列.共有：
，選B.
錯(cuò)因分析：這里是均勻分組問題.比如：第一人挑選的是周一、周二，第二人挑選的是周三、周四；也可能是第一個(gè)人挑選的是周三、周四，第二人挑選的是周一、周二，所以在全排列的過程中就重復(fù)計(jì)算了.
正解：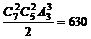
種.
4遺漏計(jì)算出錯(cuò)
在排列組合問題中還可能由于考慮問題不夠全面，因?yàn)檫z漏某些情況，而出錯(cuò)。
例6 用數(shù)字0，1，2，3，4組成沒有重復(fù)數(shù)字的比1000大的奇數(shù)共有（ ）
（A）36個(gè) （B）48個(gè) （C）66個(gè) （D）72個(gè)
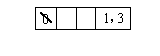誤解：如右圖，最后一位只能是1或3有兩種取法，
又因?yàn)榈?位不能是0，在最后一位取定后只有3種取
法，剩下3個(gè)數(shù)排中間兩個(gè)位置有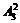
種排法，共有
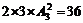個(gè).
錯(cuò)因分析：誤解只考慮了四位數(shù)的情況，而比1000大的奇數(shù)還可能是五位數(shù).
正解：任一個(gè)五位的奇數(shù)都符合要求，共有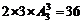
個(gè)，再由前面分析四位數(shù)個(gè)數(shù)和五位數(shù)個(gè)數(shù)之和共有72個(gè)，選D.
5忽視題設(shè)條件出錯(cuò)
在解決排列組合問題時(shí)一定要注意題目中的每一句話甚至每一個(gè)字和符號(hào)，不然就可能多解或者漏解.
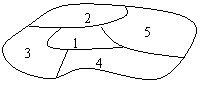
例7 (2003全國高考題)如圖，一個(gè)
地區(qū)分為5個(gè)行政區(qū)域，現(xiàn)給地圖著色，
要求相鄰區(qū)域不得使用同一顏色，現(xiàn)有4
種顏色可供選擇，則不同的著色方法共有 種.（以數(shù)字作答）
誤解：先著色第一區(qū)域，有4種方法，剩下3種顏色涂四個(gè)區(qū)域，即有一種顏色涂相對(duì)的兩塊區(qū)域，有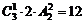
種，由乘法原理共有：
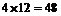種.
錯(cuò)因分析：據(jù)報(bào)導(dǎo)，在高考中有很多考生填了48種.這主要是沒有看清題設(shè)“有4種顏色可供選擇”，不一定需要4種顏色全部使用，用3種也可以完成任務(wù).
正解：當(dāng)使用四種顏色時(shí)，由前面的誤解知有48種著色方法；當(dāng)僅使用三種顏色時(shí)：從4種顏色中選取3種有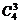
種方法，先著色第一區(qū)域，有3種方法，剩下2種顏色涂四個(gè)區(qū)域，只能是一種顏色涂第2、4區(qū)域，另一種顏色涂第3、5區(qū)域，有2種著色方法，由乘法原理有
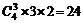種.綜上共有：
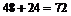種.
例8 已知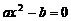
是關(guān)于
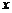的一元二次方程，其中
、
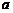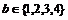，求解集不同的一元二次方程的個(gè)數(shù).
誤解：從集合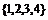
中任意取兩個(gè)元素作為
、
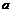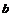，方程有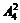
個(gè)，當(dāng)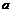、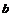取同一個(gè)數(shù)時(shí)方程有1個(gè)，共有
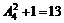個(gè).
錯(cuò)因分析：誤解中沒有注意到題設(shè)中：“求解集不同的……”所以在上述解法中要去掉同解情況，由于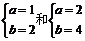
同解、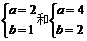
同解，故要減去2個(gè)。
正解：由分析，共有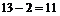
個(gè)解集不同的一元二次方程.
6未考慮特殊情況出錯(cuò)
在排列組合中要特別注意一些特殊情況，一有疏漏就會(huì)出錯(cuò).
例9 現(xiàn)有1角、2角、5角、1元、2元、5元、10元、50元人民幣各一張，100元人民幣2張，從中至少取一張，共可組成不同的幣值種數(shù)是（ ）
(A)1024種 (B)1023種 (C)1536種 (D)1535種
誤解：因?yàn)楣灿腥嗣駧?0張，每張人民幣都有取和不取2種情況，減去全不取的1種情況，共有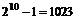
種.
錯(cuò)因分析：這里100元面值比較特殊有兩張，在誤解中被計(jì)算成 4 種情況，實(shí)際上只有不取、取一張和取二張3種情況.
正解：除100元人民幣以外每張均有取和不取2種情況，100元人民幣的取法有3種情況，再減去全不取的1種情況，所以共有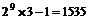
種.
7題意的理解偏差出錯(cuò)
例10 現(xiàn)有8個(gè)人排成一排照相，其中有甲、乙、丙三人不能相鄰的排法有（ ）種.
（A）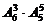
（B）
（C）
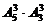（D）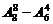
誤解：除了甲、乙、丙三人以外的5人先排，有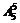
種排法，5人排好后產(chǎn)生6個(gè)空檔，插入甲、乙、丙三人有
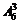種方法，這樣共有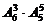種排法，選A.
錯(cuò)因分析：誤解中沒有理解“甲、乙、丙三人不能相鄰”的含義，得到的結(jié)果是“甲、乙、丙三人互不相鄰”的情況.“甲、乙、丙三人不能相鄰”是指甲、乙、丙三人不能同時(shí)相鄰，但允許其中有兩人相鄰.
正解：在8個(gè)人全排列的方法數(shù)中減去甲、乙、丙全相鄰的方法數(shù)，就得到甲、乙、丙三人不相鄰的方法數(shù)，即，故選B.
8解題策略的選擇不當(dāng)出錯(cuò)
有些排列組合問題用直接法或分類討論比較困難，要采取適當(dāng)?shù)慕鉀Q策略，如間接法、插入法、捆綁法、概率法等，有助于問題的解決.
例10 高三年級(jí)的三個(gè)班到甲、乙、丙、丁四個(gè)工廠進(jìn)行社會(huì)實(shí)踐，其中工廠甲必須有班級(jí)去，每班去何工廠可自由選擇，則不同的分配方案有（ ）.
（A）16種 （B）18種 （C）37種 （D）48種
誤解：甲工廠先派一個(gè)班去，有3種選派方法，剩下的2個(gè)班均有4種選擇，這樣共有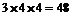
種方案.
錯(cuò)因分析：顯然這里有重復(fù)計(jì)算.如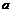：班先派去了甲工廠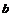，班選擇時(shí)也去了甲工廠，這與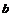班先派去了甲工廠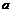，班選擇時(shí)也去了甲工廠是同一種情況，而在上述解法中當(dāng)作了不一樣的情況，并且這種重復(fù)很難排除.
正解：用間接法.先計(jì)算3個(gè)班自由選擇去何工廠的總數(shù)，再扣除甲工廠無人去的情況，即：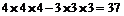
種方案.
排列組合問題雖然種類繁多，但只要能把握住最常見的原理和方法，即：“分步用乘、分類用加、有序排列、無序組合”，留心容易出錯(cuò)的地方就能夠以不變應(yīng)萬變，把排列組合學(xué)好.
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話：027-86699610 舉報(bào)郵箱：58377363@163.com