
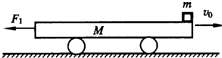
 如圖所示,平板車長L=6.0m,質量M=10kg,將其置于光滑水平面上,車的上表面距水平面h=1.25m.平板車在光滑水平面上以v0=10m/s向右做勻速直線運動,某時刻對平板車施加一個方向水平向左、大小F1=78N的恒力,與此同時,將一個質量m=1.0kg的木塊輕放在平板車右端.F1作用1.0s后,將力的大小改為F2=422N(作用位置和施力方向均不變).F2作用一段時間后,木塊脫離平板車落到平面上,在木塊脫離平板車的瞬間撤去F2.已知平板車與木塊間的動摩擦因數μ=0.20,木塊可視為質點,空氣阻力可忽略不計.求:
如圖所示,平板車長L=6.0m,質量M=10kg,將其置于光滑水平面上,車的上表面距水平面h=1.25m.平板車在光滑水平面上以v0=10m/s向右做勻速直線運動,某時刻對平板車施加一個方向水平向左、大小F1=78N的恒力,與此同時,將一個質量m=1.0kg的木塊輕放在平板車右端.F1作用1.0s后,將力的大小改為F2=422N(作用位置和施力方向均不變).F2作用一段時間后,木塊脫離平板車落到平面上,在木塊脫離平板車的瞬間撤去F2.已知平板車與木塊間的動摩擦因數μ=0.20,木塊可視為質點,空氣阻力可忽略不計.求: gt2
gt2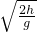 =0.50 s
=0.50 s 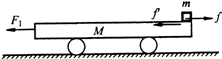
 a1t2,解得:x1=6.0 m
a1t2,解得:x1=6.0 m  a2t2=1.0 m
a2t2=1.0 m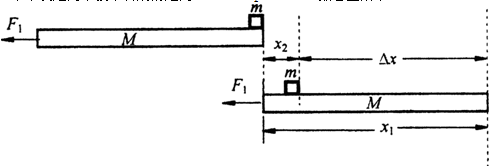

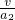 =1.0 s
=1.0 s a3t2=-19 m
a3t2=-19 m a2t2
a2t2 a3 t2
a3 t2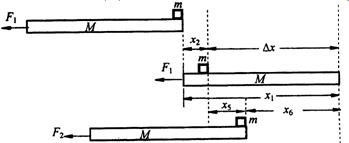


 云南師大附小一線名師提優作業系列答案
云南師大附小一線名師提優作業系列答案 沖刺100分單元優化練考卷系列答案
沖刺100分單元優化練考卷系列答案科目:高中物理 來源: 題型:
. |
| PB |
| L |
| 3 |

查看答案和解析>>
科目:高中物理 來源: 題型:
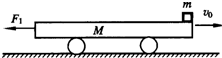 如圖所示,平板車長L=6.0m,質量M=10kg,將其置于光滑水平面上,車的上表面距水平面h=1.25m.平板車在光滑水平面上以v0=10m/s向右做勻速直線運動,某時刻對平板車施加一個方向水平向左、大小F1=78N的恒力,與此同時,將一個質量m=1.0kg的木塊輕放在平板車右端.F1作用1.0s后,將力的大小改為F2=422N(作用位置和施力方向均不變).F2作用一段時間后,木塊脫離平板車落到平面上,在木塊脫離平板車的瞬間撤去F2.已知平板車與木塊間的動摩擦因數μ=0.20,木塊可視為質點,空氣阻力可忽略不計.求:
如圖所示,平板車長L=6.0m,質量M=10kg,將其置于光滑水平面上,車的上表面距水平面h=1.25m.平板車在光滑水平面上以v0=10m/s向右做勻速直線運動,某時刻對平板車施加一個方向水平向左、大小F1=78N的恒力,與此同時,將一個質量m=1.0kg的木塊輕放在平板車右端.F1作用1.0s后,將力的大小改為F2=422N(作用位置和施力方向均不變).F2作用一段時間后,木塊脫離平板車落到平面上,在木塊脫離平板車的瞬間撤去F2.已知平板車與木塊間的動摩擦因數μ=0.20,木塊可視為質點,空氣阻力可忽略不計.求:查看答案和解析>>
科目:高中物理 來源: 題型:
. |
| PB |
| L |
| 3 |

查看答案和解析>>
科目:高中物理 來源: 題型:
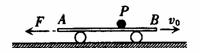
如圖所示,平板車長L=6m,質量M=10kg,上表面距離水平地面高h=1.25m,在水平面上向右做直線運動,A、B是其左右兩個端點。某時刻小車的速度v0=7.2m/s,在此時刻對平板車施加一個方向水平左的恒力F=50N,與此同時,將一個質量m=1kg的小球輕放在平板車上的P點(小球可視為質點,放在P點時相對于地面的速度為零),PB=![]() ,經過一段時間,小球脫離平板車落到地面。車與地面的動摩擦因數為0.2。其他摩擦均不計,取g=10m/s2,求:
,經過一段時間,小球脫離平板車落到地面。車與地面的動摩擦因數為0.2。其他摩擦均不計,取g=10m/s2,求:
(1)小球從離開平板車開始至落到地面所用的時間。
(2)小球從輕放到平板車開始至離開平板車所用的時間。
(3)從小球輕放上平板車至落到地面的過程中,摩擦力對平板車做的功。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com