
 如圖所示,光滑的平行金屬導軌水平放置,電阻不計,導軌間距為l,左側接一阻值為R的電阻.區域cdef內存在垂直軌道平面向下的有界勻強磁場,磁場寬度為s.一質量為m、有效電阻為r的金屬棒MN置于導軌上,與導軌垂直且接觸良好,受到F=0.5v+0.4(N)(v為金屬棒速度)的水平外力作用,從磁場的左邊界由靜止開始運動,測得電阻兩端電壓隨時間均勻增大.(已知:l=1m,m=1kg,R=0.3Ω,r=0.2Ω,s=1m)
如圖所示,光滑的平行金屬導軌水平放置,電阻不計,導軌間距為l,左側接一阻值為R的電阻.區域cdef內存在垂直軌道平面向下的有界勻強磁場,磁場寬度為s.一質量為m、有效電阻為r的金屬棒MN置于導軌上,與導軌垂直且接觸良好,受到F=0.5v+0.4(N)(v為金屬棒速度)的水平外力作用,從磁場的左邊界由靜止開始運動,測得電阻兩端電壓隨時間均勻增大.(已知:l=1m,m=1kg,R=0.3Ω,r=0.2Ω,s=1m)分析 (1)根據切割產生的感應電動勢公式以及閉合電路歐姆定律求出電阻兩端的電壓與速度的關系,從而得出速度與時間的關系,判斷出金屬棒的運動規律.
(2)根據牛頓第二定律,結合F的大小,抓住金屬棒做勻加速直線運動,a恒定,與速度無關,求出磁感應強度的大小和加速度的大小.
(3)根據R兩端的電壓U均勻增大,分析金屬棒的運動性質.U均勻增大,v均勻增大,金屬棒做勻加速運動,由運動學公式得出金屬棒勻加速運動的位移和速度與時間的關系式.撤去外力后,由題v=v0-$\frac{{B}^{2}{l}^{2}}{m(R+r)}$x,得到勻加速運動的末速度與減速運動位移的關系式,聯立求解t.
解答 解:(1)金屬棒做勻加速運動;
(2)根據牛頓第二定律有:F-F安=ma
又安培力大小為:F安=IBl,
閉合電路歐姆定律有:I=$\frac{E}{R+r}$,
切割感應電動勢為:E=Blv
可得:F-$\frac{{B}^{2}{l}^{2}}{R+r}$v=ma
將 F=0.5v+0.4代入上式
得:(0.5-$\frac{{B}^{2}{l}^{2}}{R+r}$)v+0.4=ma
即 a=(0.5-2B2)v+0.4
所以加速度為恒量,與v無關,
所以a=0.4m/s2
因為加速度為恒量,與v無關,所以有有:
(0.5-2B2)=0
得:B=0.5T
(3)設外力F作用的時間為t,力F作用下棒運動的距離為
x1=$\frac{1}{2}$at2
撤去外力F后棒運動的距離為x2,則由題設有:0=at-$\frac{{B}^{2}{l}^{2}}{m(R+r)}$x2
因 x1+x2=s
所以$\frac{1}{2}$at2+$\frac{m(R+r)}{{B}^{2}{l}^{2}}$at=s
代入數據得:0.2t2+0.8t-1=0
解方:t=1s或t=-5s(舍去).
答:
(1)金屬棒做勻加速運動;
(2)金屬棒在力F作用下運動的加速度a的大小為0.4m/s2;磁感應強度B的大小為0.5T;
(3)外力F作用的時間為1s.
點評 根據物理規律找出物理量的關系,通過已知量得出未知量.要善于對物體過程分析和進行受力分析,運用牛頓第二定律結合運動學公式解決問題.


科目:高中物理 來源: 題型:解答題
 如圖所示,P、Q為水平面內平行放置的金屬長直導軌,間距為L1=0.5m,處在磁感應強度大小為B1=0.7T、方向豎直向下的勻強磁場中,一根質量為M=0.3kg、電阻為r=1Ω的導體桿ef垂直于P、Q放在導軌上,導體桿ef與P、Q之間的動摩擦因數為μ=0.1.在外力作用下導體桿ef向左做勻速直線運動,質量為m=0.2kg、每邊電阻均為r=1Ω、邊長為L2=0.2m的正方形金屬框abcd置于豎直平面內,兩頂點a、b通過細導線與導軌相連,金屬框處在磁感應強度大小為B2=1T、方向垂直框面向里的勻強磁場中,金屬框恰好處于靜止狀態,重力加速度g=10m/s2,不計其余電阻和細導線對a、b點的作用力,求:
如圖所示,P、Q為水平面內平行放置的金屬長直導軌,間距為L1=0.5m,處在磁感應強度大小為B1=0.7T、方向豎直向下的勻強磁場中,一根質量為M=0.3kg、電阻為r=1Ω的導體桿ef垂直于P、Q放在導軌上,導體桿ef與P、Q之間的動摩擦因數為μ=0.1.在外力作用下導體桿ef向左做勻速直線運動,質量為m=0.2kg、每邊電阻均為r=1Ω、邊長為L2=0.2m的正方形金屬框abcd置于豎直平面內,兩頂點a、b通過細導線與導軌相連,金屬框處在磁感應強度大小為B2=1T、方向垂直框面向里的勻強磁場中,金屬框恰好處于靜止狀態,重力加速度g=10m/s2,不計其余電阻和細導線對a、b點的作用力,求:查看答案和解析>>
科目:高中物理 來源: 題型:計算題
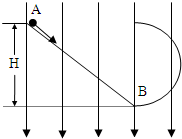 如圖所示,質量為m、帶電量為-q的小球在光滑導軌上運動,豎直半圓形滑環的半徑為R,跟斜軌在B點相切.小球在A點時的初速度為V 0,方向和斜軌平行.整個裝置放在方向豎直向下,電場強度為E的勻強電場中,斜軌的高為H,試問:
如圖所示,質量為m、帶電量為-q的小球在光滑導軌上運動,豎直半圓形滑環的半徑為R,跟斜軌在B點相切.小球在A點時的初速度為V 0,方向和斜軌平行.整個裝置放在方向豎直向下,電場強度為E的勻強電場中,斜軌的高為H,試問:查看答案和解析>>
科目:高中物理 來源: 題型:計算題

查看答案和解析>>
科目:高中物理 來源: 題型:計算題
 光滑絕緣的水平面上方存在一個水平方向的勻強電場,電場線與x軸平行,電勢φ與坐標值x的關系式:φ=1×106x(φ單位為V,x單位為m).一質量m=4×10-4kg、帶電荷量q=+2×10-8C的小滑塊P,從x=0處以初速度v0=10m/s沿x軸正方向運動.求:
光滑絕緣的水平面上方存在一個水平方向的勻強電場,電場線與x軸平行,電勢φ與坐標值x的關系式:φ=1×106x(φ單位為V,x單位為m).一質量m=4×10-4kg、帶電荷量q=+2×10-8C的小滑塊P,從x=0處以初速度v0=10m/s沿x軸正方向運動.求:查看答案和解析>>
科目:高中物理 來源: 題型:計算題
 如圖所示為示波管的結構原理圖,初速度為0的電子經U1=2500v電壓加速后,沿偏轉電揚中心軸線射入,不加偏轉電壓時,電子打在熒光屏的中心O點,設板長l=4cm,板間距d=2cm,熒光屏到偏轉板右端距離l′=16cm,熒光屏界面直徑d′=12cm試求:
如圖所示為示波管的結構原理圖,初速度為0的電子經U1=2500v電壓加速后,沿偏轉電揚中心軸線射入,不加偏轉電壓時,電子打在熒光屏的中心O點,設板長l=4cm,板間距d=2cm,熒光屏到偏轉板右端距離l′=16cm,熒光屏界面直徑d′=12cm試求:查看答案和解析>>
科目:高中物理 來源: 題型:多選題
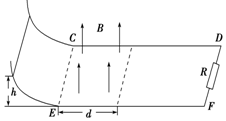 CD、EF是兩條水平放置的阻值可忽略的平行金屬導軌,導軌間距為L,在水平導軌的左側存在磁感應強度方向垂直導軌平面向上的勻強磁場,磁感應強度大小為B,磁場區域的寬度為d,如圖所示.導軌的右端接有一阻值為R的電阻,左端與一彎曲的光滑軌道平滑連接.將一阻值也為R,質量為m的導體棒從彎曲軌道上h高處由靜止釋放,導體棒最終恰好停在磁場的右邊界處.已知導體棒與水平導軌接觸良好,且動摩擦因數為μ,則下列說法中正確的是( )
CD、EF是兩條水平放置的阻值可忽略的平行金屬導軌,導軌間距為L,在水平導軌的左側存在磁感應強度方向垂直導軌平面向上的勻強磁場,磁感應強度大小為B,磁場區域的寬度為d,如圖所示.導軌的右端接有一阻值為R的電阻,左端與一彎曲的光滑軌道平滑連接.將一阻值也為R,質量為m的導體棒從彎曲軌道上h高處由靜止釋放,導體棒最終恰好停在磁場的右邊界處.已知導體棒與水平導軌接觸良好,且動摩擦因數為μ,則下列說法中正確的是( )| A. | 電阻R的最大電流為$\frac{BL\sqrt{2gh}}{2R}$ | B. | 流過電阻R的電荷量為$\frac{BdL}{2R}$ | ||
| C. | 整個電路中產生的焦耳熱為mgh | D. | 電阻R中產生的焦耳熱為$\frac{1}{2}$mg(h-μd) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com