
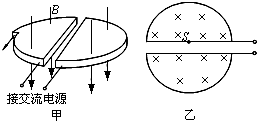
 在高能物理研究中,粒子加速器起著重要作用,而早期的加速器只能使帶電粒子在高壓電場中加速一次,因而粒子所能達到的能量受到高壓技術的限制.1930年,Earnest O.Lawrence提出了回旋加速器的理論,他設想用磁場使帶電粒子沿圓弧形軌道旋轉,多次反復地通過高頻加速電場,直至達到高能量.圖甲為Earnest O.Lawrence設計的回旋加速器的示意圖.它由兩個鋁制D型金屬扁盒組成,兩個D形盒正中間開有一條狹縫;兩個D型盒處在勻強磁場中并接有高頻交變電壓.圖乙為俯視圖,在D型盒上半面中心S處有一正離子源,它發出的正離子,經狹縫電壓加速后,進入D型盒中.在磁場力的作用下運動半周,再經狹縫電壓加速;為保證粒子每次經過狹縫都被加速,應設法使交變電壓的周期與粒子在狹縫及磁場中運動的周期一致.如此周而復始,最后到達D型盒的邊緣,獲得最大速度后被束流提取裝置提取出.已知正離子的電荷量為q,質量為m,加速時電極間電壓大小恒為U,磁場的磁感應強度為B,D型盒的半徑為R,狹縫之間的距離為d.設正離子從離子源出發時的初速度為零.
在高能物理研究中,粒子加速器起著重要作用,而早期的加速器只能使帶電粒子在高壓電場中加速一次,因而粒子所能達到的能量受到高壓技術的限制.1930年,Earnest O.Lawrence提出了回旋加速器的理論,他設想用磁場使帶電粒子沿圓弧形軌道旋轉,多次反復地通過高頻加速電場,直至達到高能量.圖甲為Earnest O.Lawrence設計的回旋加速器的示意圖.它由兩個鋁制D型金屬扁盒組成,兩個D形盒正中間開有一條狹縫;兩個D型盒處在勻強磁場中并接有高頻交變電壓.圖乙為俯視圖,在D型盒上半面中心S處有一正離子源,它發出的正離子,經狹縫電壓加速后,進入D型盒中.在磁場力的作用下運動半周,再經狹縫電壓加速;為保證粒子每次經過狹縫都被加速,應設法使交變電壓的周期與粒子在狹縫及磁場中運動的周期一致.如此周而復始,最后到達D型盒的邊緣,獲得最大速度后被束流提取裝置提取出.已知正離子的電荷量為q,質量為m,加速時電極間電壓大小恒為U,磁場的磁感應強度為B,D型盒的半徑為R,狹縫之間的距離為d.設正離子從離子源出發時的初速度為零.分析 (1)根據動能定理求出粒子被第一次加速后的速度,根據洛倫茲力提供向心力,利用牛頓第二定律求出軌道的半徑.
(2)回旋加速器是利用電場加速和磁場偏轉來加速粒子,根據動能定理求出n次加速后的速度,根據勻變速直線運動的速度時間公式求出加速的時間,再求出粒子偏轉的次數,從而得出在磁場中偏轉的時間,兩個時間之和即為離開離子源到被第n次加速結束時所經歷的時間.
(3)根據回旋加速器的半徑,利用洛倫茲力提供向心力,求出最大速度,看最大速度有什么因素決定.
解答 解:(1)設正離子經過窄縫被第一次加速加速后的速度為v1,由動能定理得$qU=\frac{1}{2}mv_1^2$
正離子在磁場中做勻速圓周運動,半徑為r1,由牛頓第二定律得:$Bq{v_1}=m\frac{{{v_1}^2}}{r_1}$
由以上兩式解得:${r_1}=\sqrt{\frac{2mU}{{q{B^2}}}}$
(2)設正離子經過窄縫被第n次加速加速后的速度為vn,由動能定理得:$nqU=\frac{1}{2}mv_n^2$
粒子在狹縫中經n次加速的總時間:${t_1}=\frac{v_n}{a}$(1分);由牛頓第二定律:$q\frac{U}p9vv5xb5=ma$
由以上三式解得電場對粒子加速的時間:${t_1}=d\sqrt{\frac{2nm}{qU}}$
正離子在磁場中做勻速圓周運動,由牛頓第二定律:$Bqv=m\frac{v^2}{r}$
又:$T=\frac{2πr}{v}$
粒子在磁場中做圓周運動的時間:${t_2}=(n-1)\frac{T}{2}$
由以上三式解得 ${t_2}=\frac{(n-1)πm}{qB}$
所以,粒子從離開離子源到被第n次加速結束時所經歷的時間$t=t_1^{\;}+{t_2}$=$d\sqrt{\frac{2nm}{qU}}$+$\frac{(n-1)πm}{qB}$
(3)設離子從D盒邊緣離開時做圓周運動的軌跡半徑為rm,速度為vmrm=R; $Bq{v_m}=m\frac{{{v_m}^2}}{r_m}$
離子獲得的最大動能為:$E=\frac{1}{2}mv_m^2=\frac{{{q^2}{B^2}{R^2}}}{2m}$
所以,要提高某一離子被半徑為R的回旋加速器加速后的最大動能可以增大加速器中的磁感應強度B.
答:(1)上述正離子從離子源出發被第一次加速后進入下半盒中運動的軌道半徑$\sqrt{\frac{2mU}{q{B}^{2}}}$;
(2)正離子在某次加速過程當中從離開離子源到被第n次加速結束時所經歷的時間$d\sqrt{\frac{2nm}{qU}}$+$\frac{(n-1)πm}{qB}$;
(3)要提高某一離子被半徑為R的回旋加速器加速后的最大動能可以增大加速器中的磁感應強度B.
點評 解決本題的關鍵知道帶電粒子在磁場中偏轉規律在回旋加強器的工作原理,利用磁場偏轉,電場加速.以及知道回旋加強器加速粒子的最大動能與什么因素有關進行分析,明確在電場和磁場中運動時間的計算方法.


科目:高中物理 來源: 題型:選擇題
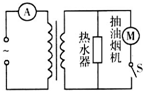 如圖,理想變壓器原線圈接交流電源,副線圈接熱水器和抽油煙機,原副線圈的匝數比為5:1,副線圈上電源的瞬時值u=220$\sqrt{2}$sin100πt(V),開關S斷開時,電流表示數是1A,開關S閉合時,電流表示數是1.2A,下列說法正確的是( )
如圖,理想變壓器原線圈接交流電源,副線圈接熱水器和抽油煙機,原副線圈的匝數比為5:1,副線圈上電源的瞬時值u=220$\sqrt{2}$sin100πt(V),開關S斷開時,電流表示數是1A,開關S閉合時,電流表示數是1.2A,下列說法正確的是( )| A. | S閉合時,抽油煙機消耗的功率是220W | |
| B. | 交流電源輸出電壓的最大值是1100V | |
| C. | S閉合時,熱水器消耗的功率減小 | |
| D. | S閉合時,熱水器消耗的功率是220W |
查看答案和解析>>
科目:高中物理 來源: 題型:解答題
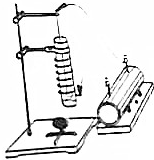 在玻璃管中心軸上安裝一根指導線,玻璃管外繞有線圈,直導線的一端和線圈的一端分別跟感應圈的兩放電柱相連,開始,感應圈未接通電源,點燃蚊香,讓煙通過玻璃管冒出,當感應圈電源接通時,玻璃管中的導線和管外線圈間就會加上高電壓,立即可以看到,不再有煙從玻璃管中冒出來了.過一會兒還可以看到管壁吸附了一層煙塵,請思考一下:這是什么原因?
在玻璃管中心軸上安裝一根指導線,玻璃管外繞有線圈,直導線的一端和線圈的一端分別跟感應圈的兩放電柱相連,開始,感應圈未接通電源,點燃蚊香,讓煙通過玻璃管冒出,當感應圈電源接通時,玻璃管中的導線和管外線圈間就會加上高電壓,立即可以看到,不再有煙從玻璃管中冒出來了.過一會兒還可以看到管壁吸附了一層煙塵,請思考一下:這是什么原因?查看答案和解析>>
科目:高中物理 來源: 題型:多選題
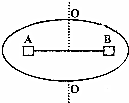 如圖所示,水平圓盤繞中心豎直軸OO′勻速轉動,在圓盤上沿半徑方向放置兩個質量分別為m1、m2的小物體A和B,小物體間用一過于圓盤中心且平行于圓盤的細線連接.已知A、B距圓盤中心距離相同,A、B與圓盤間的動摩擦因數也相同(設最大靜摩擦力等于滑動摩擦力),但m1<m2,在兩小物體隨圓盤一起勻速轉動的過程中,下列說法正確的是( )
如圖所示,水平圓盤繞中心豎直軸OO′勻速轉動,在圓盤上沿半徑方向放置兩個質量分別為m1、m2的小物體A和B,小物體間用一過于圓盤中心且平行于圓盤的細線連接.已知A、B距圓盤中心距離相同,A、B與圓盤間的動摩擦因數也相同(設最大靜摩擦力等于滑動摩擦力),但m1<m2,在兩小物體隨圓盤一起勻速轉動的過程中,下列說法正確的是( )| A. | 細線中的張力可能為零 | |
| B. | 物體A受到的摩擦力一定指向圓心 | |
| C. | 物體A受到的摩擦力可能背離圓心 | |
| D. | A、B兩物體的向心加速度大小始終相同 |
查看答案和解析>>
科目:高中物理 來源: 題型:解答題
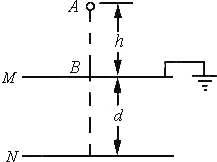 如圖所示,兩塊水平放置的平行金屬板M、N相距為d,組成一個電容為C的平行板電容器,M板接地,M板接地,板正中央有一小孔B,從B孔正上方的h處的A點,一滴一滴地由靜止滴下質量為m、電荷量為q的帶電油滴,油滴穿過B孔后落到N板,把全部電荷量傳給N板,若不計空氣阻力及板外電場,問:
如圖所示,兩塊水平放置的平行金屬板M、N相距為d,組成一個電容為C的平行板電容器,M板接地,M板接地,板正中央有一小孔B,從B孔正上方的h處的A點,一滴一滴地由靜止滴下質量為m、電荷量為q的帶電油滴,油滴穿過B孔后落到N板,把全部電荷量傳給N板,若不計空氣阻力及板外電場,問:查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
| A. | 曲線運動的加速度可以為零 | |
| B. | 做曲線運動的物體所受合力可以為零 | |
| C. | 曲線運動的物體所受合力方向與速度方向在同一條直線上 | |
| D. | 曲線運動的物體在某點的速度方向即為該點的切線方向 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com