

 T時刻進入復合場,與物塊碰后做勻速圓周運動,恰能垂直于邊界GH返回低一級平臺上,返回低一級臺階的過程,磁場方向與小球進入復合場時磁場方向相反,說明小球從高一級平臺進入復合場到與物塊碰撞經過的時間等于
T時刻進入復合場,與物塊碰后做勻速圓周運動,恰能垂直于邊界GH返回低一級平臺上,返回低一級臺階的過程,磁場方向與小球進入復合場時磁場方向相反,說明小球從高一級平臺進入復合場到與物塊碰撞經過的時間等于 ,由小球做勻速圓周運動的周期公式T′=
,由小球做勻速圓周運動的周期公式T′= 即可求出交變磁場變化的周期T;
即可求出交變磁場變化的周期T; ------------------------②
------------------------②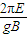 --------------------------
-------------------------- ------------------------------③
------------------------------③ ----------------------------------④
----------------------------------④ -----------------------------------⑤
-----------------------------------⑤ =
= ,又根據r=
,又根據r=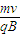 可得:則V=
可得:則V= --------⑥
--------⑥ mv2=
mv2= mV2+
mV2+ MVm2--------------------------------⑧
MVm2--------------------------------⑧ MVm2------------------------------------⑩
MVm2------------------------------------⑩ -3μmgS
-3μmgS ;
; ;
; -3μmgS.
-3μmgS.

 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案科目:高中物理 來源: 題型:
查看答案和解析>>
科目:高中物理 來源: 題型:

查看答案和解析>>
科目:高中物理 來源: 題型:

查看答案和解析>>
科目:高中物理 來源: 題型:
如圖1-3-13所示,有兩個質量相同的小球A和B(大小不計),A球用細繩吊起,細繩長度等于懸點距地面的高度,B點靜止放于懸點正下方的地面上,現將A球拉到距地面高度為h處由靜止釋放,擺動到最低點與B球碰撞后粘在一起共同上擺,則它們升起的最大高度為( )

圖1-3-13
A.h/2 B.h C.h/4 D.h/![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com