
 如圖所示,在水平長直的軌道上,有一長度為L的平板車在外力控制下始終保持速度v0做勻速直線運動.某時刻將一質量為m,可視為質點的小滑塊輕放到車面距右端
如圖所示,在水平長直的軌道上,有一長度為L的平板車在外力控制下始終保持速度v0做勻速直線運動.某時刻將一質量為m,可視為質點的小滑塊輕放到車面距右端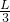 的c處,滑塊剛好停在小車左端A處,設定平板車上表面各處粗糙程度相同.
的c處,滑塊剛好停在小車左端A處,設定平板車上表面各處粗糙程度相同. ,小物塊運動的時間t=
,小物塊運動的時間t=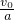 ,當小物塊的速度和車的速度相同時有根據幾何關系有:
,當小物塊的速度和車的速度相同時有根據幾何關系有: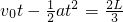 代入:a=
代入:a= 和t=
和t=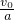 可得:
可得: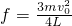
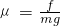 =
=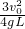
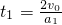 ①
① =
= ②
②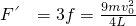 ,
,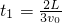
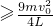
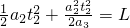 ⑥
⑥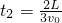
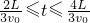
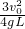 ;
;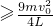
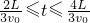 .
.

科目:高中物理 來源: 題型:
 如圖所示,在水平長直的軌道上,有一長度為L的平板車在外力控制下始終保持速度v0做勻速直線運動.某時刻將一質量為m,可視為質點的小滑塊輕放到車面距右端
如圖所示,在水平長直的軌道上,有一長度為L的平板車在外力控制下始終保持速度v0做勻速直線運動.某時刻將一質量為m,可視為質點的小滑塊輕放到車面距右端| L | 3 |
查看答案和解析>>
科目:高中物理 來源: 題型:

查看答案和解析>>
科目:高中物理 來源: 題型:
 如圖所示,在水平長直的軌道上,有一長度為L的平板車在外力控制下始終保持速度v0,做勻速直線運動.某時刻將一質量為m,可視為質點的小滑塊輕放到車面距右端
如圖所示,在水平長直的軌道上,有一長度為L的平板車在外力控制下始終保持速度v0,做勻速直線運動.某時刻將一質量為m,可視為質點的小滑塊輕放到車面距右端| L | 3 |
查看答案和解析>>
科目:高中物理 來源: 題型:
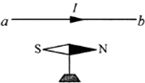 如圖所示,在水平長直導線的正下方,有一只可以自由轉動的小磁針.現給直導線通以由 a向b的恒定電流I,若地磁場的影響可忽略,則小磁針的N極將( )
如圖所示,在水平長直導線的正下方,有一只可以自由轉動的小磁針.現給直導線通以由 a向b的恒定電流I,若地磁場的影響可忽略,則小磁針的N極將( )| A、保持不動 | B、向下轉動 | C、垂直紙面向里轉動 | D、垂直紙面向外轉動 |
查看答案和解析>>
科目:高中物理 來源:2011年重慶市高考物理考前沖刺試卷(解析版) 題型:解答題
 如圖所示,在水平長直的軌道上,有一長度為L的平板車在外力控制下始終保持速度v,做勻速直線運動.某時刻將一質量為m,可視為質點的小滑塊輕放到車面距右端
如圖所示,在水平長直的軌道上,有一長度為L的平板車在外力控制下始終保持速度v,做勻速直線運動.某時刻將一質量為m,可視為質點的小滑塊輕放到車面距右端 的c處,滑塊剛好停在小車左端A處,設定平板車上表面各處粗糙程度相同.
的c處,滑塊剛好停在小車左端A處,設定平板車上表面各處粗糙程度相同.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com