

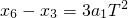 ①
①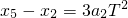 ②
②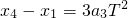 ③
③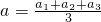 =
=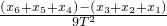 =0.63m/s2
=0.63m/s2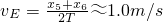


科目:高中物理 來源: 題型:

查看答案和解析>>
科目:高中物理 來源: 題型:閱讀理解
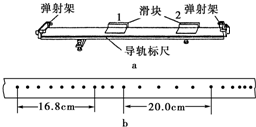 (2009?肇慶一模)某同學利用打點計時器和氣墊導軌做驗證動量守恒定律的實驗.氣墊導軌裝置如圖a所示,所用的氣墊導軌裝置由導軌、滑塊、彈射架等組成.在空腔導軌的兩個工作面上均勻分布著一定數量的小孔,向導軌空腔內不斷通入壓縮空氣,空氣會從小孔中噴出,使滑塊穩定地漂浮在導軌上,這樣就大大減小了因滑塊和導軌之間的摩擦而引起的誤差.
(2009?肇慶一模)某同學利用打點計時器和氣墊導軌做驗證動量守恒定律的實驗.氣墊導軌裝置如圖a所示,所用的氣墊導軌裝置由導軌、滑塊、彈射架等組成.在空腔導軌的兩個工作面上均勻分布著一定數量的小孔,向導軌空腔內不斷通入壓縮空氣,空氣會從小孔中噴出,使滑塊穩定地漂浮在導軌上,這樣就大大減小了因滑塊和導軌之間的摩擦而引起的誤差.查看答案和解析>>
科目:高中物理 來源: 題型:
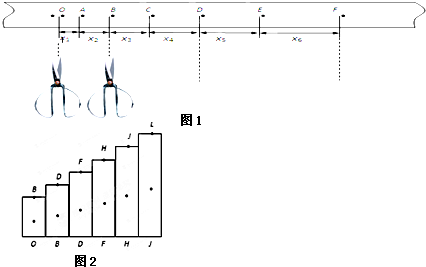
查看答案和解析>>
科目:高中物理 來源: 題型:

查看答案和解析>>
科目:高中物理 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com