
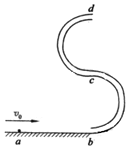
 如圖所示的“s”形玩具軌道,該軌道是用內壁光滑的薄壁細圓管彎成,放置在豎直平面內,軌道彎曲部分是由兩個半徑相等的半圓對接而成,圓半徑比細管內徑大得多,軌道底端與水平地面相切,軌道在水平方向不可移動.彈射裝置將一個小球(小球的直徑略小于細圓管內徑)從a點沿水平地面向b點運動并進入軌道,經過軌道后從最高點d水平拋出.已知小球與地面ab段間的動摩擦因數為μ,ab段長L,圓的半徑R,小球質量m,求:
如圖所示的“s”形玩具軌道,該軌道是用內壁光滑的薄壁細圓管彎成,放置在豎直平面內,軌道彎曲部分是由兩個半徑相等的半圓對接而成,圓半徑比細管內徑大得多,軌道底端與水平地面相切,軌道在水平方向不可移動.彈射裝置將一個小球(小球的直徑略小于細圓管內徑)從a點沿水平地面向b點運動并進入軌道,經過軌道后從最高點d水平拋出.已知小球與地面ab段間的動摩擦因數為μ,ab段長L,圓的半徑R,小球質量m,求:分析 (1)根據牛頓第二定律與機械能守恒定律,即可求解;
(2)根據平拋運動規律處理的方法,運用牛頓第二定律與運動學公式綜合,借助于幾何關系,即可求解;根據動能定理,與牛頓第二定律,結合向心力表達式,即可求解.
解答 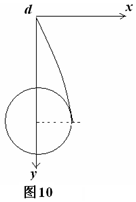 解:(1)根據牛頓第二定律,小球經d點時
解:(1)根據牛頓第二定律,小球經d點時
Fd+mg=m$\frac{{v}_p9vv5xb5^{2}}{R}$
Fd>0
即vd$>\sqrt{gR}$
小球從b到d,由機械能守恒定律
$\frac{1}{2}$mvd2+4mgR=$\frac{1}{2}$mvb2
解得vb$>3\sqrt{gR}$
(2)假設恰好落到豎直位移3R處,則該點的速度方向豎直向下,這不符合平拋運動的規律.設小球離開d出時的速度為vd時,在運動過程中與軌道恰好相碰,即小球的運動軌跡與圓相切.以d點為坐標原點建立如圖坐標系,由平拋運動規律得
x=vat
y=$\frac{1}{2}g{t}^{2}$ ②
由①②兩式得y=$\frac{g}{2{v}_p9vv5xb5^{2}}{x}^{2}$ ③
由解析幾何知識得x2+(y-3R)2=R2 ④
聯立③④兩式得y2+($\frac{2{v}_p9vv5xb5^{2}}{g}$-6R)y+8R2=0 ⑤
要使的拋物線與圓相切,則方程⑤的△判別式為零,即
△=($\frac{2{v}_p9vv5xb5^{2}}{g}$-6R)2-32R2=0
解得:vd=$\sqrt{(3-2\sqrt{2})gR}$
故小球離開軌道d處后,不再碰到軌道,小球離開d出時的速度至少為$\sqrt{(3-2\sqrt{2})gR}$
答:(1)若小球經d處時,對軌道上臂有壓力,則它經過b處時的速度滿足vb$>3\sqrt{gR}$
(2)為使小球離開軌道d處后,不會再碰到軌道,則小球離開d出時的速度至少為$\sqrt{(3-2\sqrt{2})gR}$
點評 本題考查動能定理、機械能守恒定律、牛頓第二定律與運動學公式等規律的應用,知道向心力的表達式,同時注意受力分析的研究對象確定,本題同時還要注意數學規律的基本應用.


科目:高中物理 來源: 題型:計算題
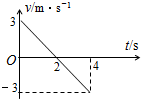 你可能到公園或游樂園蹦床.如圖所示是一同學某次蹦床跳起后的v-t圖象,結合你的體會和經歷,回答下列問題:
你可能到公園或游樂園蹦床.如圖所示是一同學某次蹦床跳起后的v-t圖象,結合你的體會和經歷,回答下列問題:查看答案和解析>>
科目:高中物理 來源: 題型:多選題
| A. | 三個公式都只能在真空中適用 | |
| B. | 公式②能在真空中適用,公式①和③在真空中和介質中都適用 | |
| C. | 公式①適用于任何電場 | |
| D. | 公式②只適用于真空中點電荷形成的電場,公式③只適用于勻強電場 |
查看答案和解析>>
科目:高中物理 來源: 題型:多選題
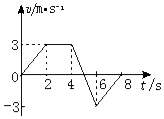
| A. | 0<t<2 s | B. | 4 s<t<5s | C. | 5s<t<6s | D. | 6s<t<8s |
查看答案和解析>>
科目:高中物理 來源: 題型:實驗題
查看答案和解析>>
科目:高中物理 來源: 題型:實驗題
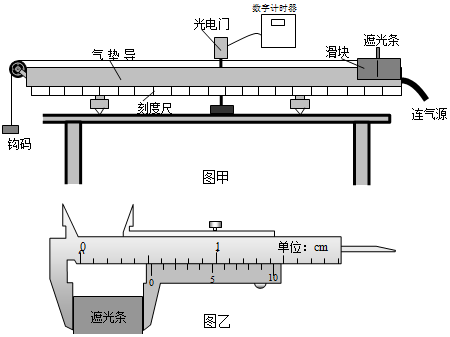
 某同學在“用打點計時器測速度”的實驗中,用打點計時器記錄了被小車拖動的紙帶的運動情況,在紙帶上確定出0、1、2、3、4、5、6共7個測量點,每兩個相鄰的測量點之間還有四個點沒標出,其部分相鄰點間的距離如圖所示,完成下列問題.
某同學在“用打點計時器測速度”的實驗中,用打點計時器記錄了被小車拖動的紙帶的運動情況,在紙帶上確定出0、1、2、3、4、5、6共7個測量點,每兩個相鄰的測量點之間還有四個點沒標出,其部分相鄰點間的距離如圖所示,完成下列問題.查看答案和解析>>
科目:高中物理 來源: 題型:多選題
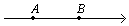
| A. | EA>EB,φA>φB | B. | EA>EB,φA與φB無法判斷大小 | ||
| C. | EA與EB無法判斷大小,φA>φB | D. | 可能有EA=EB,φA>φB |
查看答案和解析>>
科目:高中物理 來源: 題型:解答題
 如圖所示,固定于水平面上、傾角θ=37°的光滑斜面底端固定一與斜面偏小的輕彈簧,勁度系數k=40N/m.將一質量為m=0.2kg的物塊(可視為質點),放置在質量M=0.8kg的木板上,木板和物塊一起自斜面頂端由靜止釋放.當木板的下端到達A點時,彈簧的壓縮量x1=0.1m,木板正處在加速下滑的過程中,速度v0=1m/s,此時物塊剛好相對木板開始滑動;木板繼續向下運動,其下端到達B點時,木板處于平衡狀態,物塊恰好將滑離木板(滑離后物塊未觸及彈簧和斜面).設物塊與木板間的最大靜摩擦力等于滑動摩擦力,取g=10m/s2,sin37°=0.6,cos37°=0.8,求:
如圖所示,固定于水平面上、傾角θ=37°的光滑斜面底端固定一與斜面偏小的輕彈簧,勁度系數k=40N/m.將一質量為m=0.2kg的物塊(可視為質點),放置在質量M=0.8kg的木板上,木板和物塊一起自斜面頂端由靜止釋放.當木板的下端到達A點時,彈簧的壓縮量x1=0.1m,木板正處在加速下滑的過程中,速度v0=1m/s,此時物塊剛好相對木板開始滑動;木板繼續向下運動,其下端到達B點時,木板處于平衡狀態,物塊恰好將滑離木板(滑離后物塊未觸及彈簧和斜面).設物塊與木板間的最大靜摩擦力等于滑動摩擦力,取g=10m/s2,sin37°=0.6,cos37°=0.8,求:查看答案和解析>>
科目:高中物理 來源: 題型:計算題
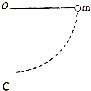 如圖所示,質量為2m、電量為+q的帶電小球A固定于一不可伸長的絕緣細線一端O點,繩的另一端有一電荷量為+Q質量為m的小球B,繩長為l,將小球拉起至與球A等高的位置后無初速度釋放.
如圖所示,質量為2m、電量為+q的帶電小球A固定于一不可伸長的絕緣細線一端O點,繩的另一端有一電荷量為+Q質量為m的小球B,繩長為l,將小球拉起至與球A等高的位置后無初速度釋放.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com