
 如圖所示,一質量m=2kg的小型四旋翼遙控無人機從地面由靜止開始豎直向上勻加速起飛,經時間t1=6s時的速度大小v1=6m/s.之后,控制遙控器使無人機立即失去升力,當無人機下落到離地面某一高度時控制遙控器使無人機立即獲得與上升時大小相等的升力,結果無人機落回地面時的速度恰好為零,已知無人機上升,下落過程中均受到大小恒為f=4N的空氣阻力,取g=10m/s2,求
如圖所示,一質量m=2kg的小型四旋翼遙控無人機從地面由靜止開始豎直向上勻加速起飛,經時間t1=6s時的速度大小v1=6m/s.之后,控制遙控器使無人機立即失去升力,當無人機下落到離地面某一高度時控制遙控器使無人機立即獲得與上升時大小相等的升力,結果無人機落回地面時的速度恰好為零,已知無人機上升,下落過程中均受到大小恒為f=4N的空氣阻力,取g=10m/s2,求分析 (1)根據速度時間關系求出無人機勻加速上升的加速度大小,根據牛頓第二定律求解升力大小;
(2)根據運動學公式計算在0~t1時間內無人機上升的高度,失去升力后根據牛頓第二定律求解加速度大小,再根據速度位移關系求解上升的高度,由此求出總的高度;
(3)根據牛頓第二定律求出下落過程中沒有升力時的加速度和恢復升力時的加速度,再根據速度位移關系列方程求解恢復升力時的速度大小.
解答 解:(1)設無人機勻加速上升的加速度大小為a1,則有:v1=a1t1,
代入數據解得:a1=1m/s2;
根據牛頓第二定律可得:F-mg-f=ma1,
代入數據解得:F=26N;
(2)在0~t1時間內,無人機上升的高度為:${h}_{1}=\frac{{v}_{1}}{2}{t}_{1}=18m$,
設無人機失去升力后繼續勻減速上升的加速度大小為a2,則有:mg+f=ma2,
代入數據解得:a2=12m/s2,
設該過程無人機上升的高度為h2,則有:v12=2a2h2,
代入數據解得:h2=1.5m;
所以上升的高度為:H=h1+h2=19.5m;
(3)設無人機恢復升力前從最大高度處下落的高度為h3,加速度大小為a3,則有:mg-f=ma3,
代入數據解得:a3=8m/s2,
根據速度位移關系可得:v22=2a3h3,
設無人機恢復升力后下落的高度為h4,加速度大小為a4,則有:F+f-mg=ma4,
代入數據解得:a4=5m/s2,
根據速度位移關系可得:v22=2a4h4,
又h3+h4=H,
聯立并代入數據解得:v2=$2\sqrt{30}m/s$.
答:(1)無人機在0~t1時間內受到的升力大小為26N;
(2)無人機上升的最大高度為19.5m;
(3)無人機再次獲得升力時的速度大小為$2\sqrt{30}m/s$.
點評 對于牛頓第二定律的綜合應用問題,關鍵是弄清楚物體的運動過程和受力情況,利用牛頓第二定律或運動學的計算公式求解加速度,再根據題目要求進行解答;知道加速度是聯系靜力學和運動學的橋梁;解答本題的關鍵是弄清楚運動過程和受力情況.


科目:高中物理 來源: 題型:計算題
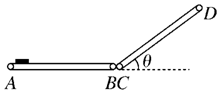 圖示為倉庫中常用的皮帶傳輸裝置示意圖,它由兩臺皮帶傳送機組成,一臺水平傳送,A、B兩端相距3m,另一臺傾斜,其傳送帶與地面的傾角θ=37°,C、D兩端相距4.45m,B、C相距很近.水平部分AB以v0=5m/s的速率順時針轉動.將一袋質量為10kg的大米無初速度放在A端,到達B端后,米袋繼續沿傾斜的CD部分運動,不計米袋在BC處的機械能損失.已知米袋與傳送帶間的動摩擦因數均為0.5,g=10m/s2,cos 37°=0.8,求:若CD部分傳送帶不運轉,米袋能否運動到D端?
圖示為倉庫中常用的皮帶傳輸裝置示意圖,它由兩臺皮帶傳送機組成,一臺水平傳送,A、B兩端相距3m,另一臺傾斜,其傳送帶與地面的傾角θ=37°,C、D兩端相距4.45m,B、C相距很近.水平部分AB以v0=5m/s的速率順時針轉動.將一袋質量為10kg的大米無初速度放在A端,到達B端后,米袋繼續沿傾斜的CD部分運動,不計米袋在BC處的機械能損失.已知米袋與傳送帶間的動摩擦因數均為0.5,g=10m/s2,cos 37°=0.8,求:若CD部分傳送帶不運轉,米袋能否運動到D端?查看答案和解析>>
科目:高中物理 來源: 題型:計算題
 將一架物理天平調節好平衡,然后將質量為m=2×10-2kg的矩形線圈abcd掛在天平托盤底部,底邊bc置于垂直紙面向里的勻強磁場中,bc=0.1m,如圖所示,在天平左盤加上適當的砝碼,使天平重新平衡.現在給線圈通以方向為adcba、大小為I=10A的電流,發現這時要在天平左盤上再加上適當的砝碼,才能使天平再一次平衡,最終左盤砝碼的總質量為M=6×10-2kg.求:(g=10m/s2)
將一架物理天平調節好平衡,然后將質量為m=2×10-2kg的矩形線圈abcd掛在天平托盤底部,底邊bc置于垂直紙面向里的勻強磁場中,bc=0.1m,如圖所示,在天平左盤加上適當的砝碼,使天平重新平衡.現在給線圈通以方向為adcba、大小為I=10A的電流,發現這時要在天平左盤上再加上適當的砝碼,才能使天平再一次平衡,最終左盤砝碼的總質量為M=6×10-2kg.求:(g=10m/s2)查看答案和解析>>
科目:高中物理 來源: 題型:實驗題
查看答案和解析>>
科目:高中物理 來源: 題型:計算題
 上調節油門后,發動機產生的牽引力為1.4×104N,小轎車的質量為2噸,小轎車與斜坡及水平地面間的動
上調節油門后,發動機產生的牽引力為1.4×104N,小轎車的質量為2噸,小轎車與斜坡及水平地面間的動查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
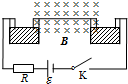 如圖所示,一段質量為m的銅導線彎成Π形,它的水平部分長為l處于磁感應強度為B、方向垂直于紙面向里的勻強磁場中.導線的兩端豎直部分的下端插入兩汞槽內液面下h,兩汞槽通過導線分別與內阻可忽略,電動勢為ε的電源正負極連接,電路中的電阻為R.合上開關K,當電動勢ε足夠大時,在磁場的作用下導線便從汞槽內跳離,切斷電路.導線上升到一定高度后又開始下落,當導線的下端接觸到汞液體后,電路重新接通,在磁場的作用下,導線下落速度逐漸降至零.此后,該段導線又重復上述運動過程,形成周期運動.忽略導線和汞液體的電阻,并設h較小,導線在磁場中運動時的電磁感應亦可忽略,則在一個周期內電源做功為( )
如圖所示,一段質量為m的銅導線彎成Π形,它的水平部分長為l處于磁感應強度為B、方向垂直于紙面向里的勻強磁場中.導線的兩端豎直部分的下端插入兩汞槽內液面下h,兩汞槽通過導線分別與內阻可忽略,電動勢為ε的電源正負極連接,電路中的電阻為R.合上開關K,當電動勢ε足夠大時,在磁場的作用下導線便從汞槽內跳離,切斷電路.導線上升到一定高度后又開始下落,當導線的下端接觸到汞液體后,電路重新接通,在磁場的作用下,導線下落速度逐漸降至零.此后,該段導線又重復上述運動過程,形成周期運動.忽略導線和汞液體的電阻,并設h較小,導線在磁場中運動時的電磁感應亦可忽略,則在一個周期內電源做功為( )| A. | ε2$\sqrt{\frac{2hm}{BεlR-mg{R}^{2}}}$ | B. | ε2$\sqrt{\frac{hm}{BεlR-mg{R}^{2}}}$ | C. | 2ε2$\sqrt{\frac{2hm}{BεlR-mg{R}^{2}}}$ | D. | 2ε2$\sqrt{\frac{hm}{BεlR-mg{R}^{2}}}$ |
查看答案和解析>>
科目:高中物理 來源: 題型:多選題
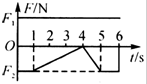 在光滑水平面上,有一個物體同時受到兩個水平力F1與F2的作用,在第1s內物體保持靜止狀態.若力F1、F2隨時間的變化如圖所示.則物體( )
在光滑水平面上,有一個物體同時受到兩個水平力F1與F2的作用,在第1s內物體保持靜止狀態.若力F1、F2隨時間的變化如圖所示.則物體( )| A. | 在第2s內做加速運動,加速度大小逐漸減小,速度逐漸增大 | |
| B. | 在第3s內做加速運動,加速度大小逐漸增大,速度逐漸增大 | |
| C. | 在第4s內做加速運動,加速度大小逐漸增大,速度逐漸增大 | |
| D. | 在第5s末加速度為零,運動方向與F1方向相反 |
查看答案和解析>>
科目:高中物理 來源: 題型:多選題
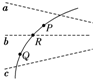 如圖所示,虛線a、b、c代表電場中的三個等勢面,相鄰等勢面之間的電勢差相等,即Uab=Ubc,實線為一帶負電的質點僅在電場力作用下通過該區域時的運動軌跡,P、R、Q是這條軌跡上的三點,R同時在等勢面b上,據此可知( )
如圖所示,虛線a、b、c代表電場中的三個等勢面,相鄰等勢面之間的電勢差相等,即Uab=Ubc,實線為一帶負電的質點僅在電場力作用下通過該區域時的運動軌跡,P、R、Q是這條軌跡上的三點,R同時在等勢面b上,據此可知( )| A. | 三個等勢面中,c的電勢最高 | |
| B. | 帶電質點在P點的電勢能比在Q點的小 | |
| C. | 帶電質點在P點的動能與電勢能之和比在Q點的小 | |
| D. | 帶電質點在R點的加速度方向垂直于等勢面b |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com