
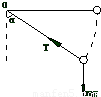
 在下落過程中繩子拉力T逐漸增大,根據力的獨立作用原理,在豎直方向上有
在下落過程中繩子拉力T逐漸增大,根據力的獨立作用原理,在豎直方向上有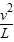 …②
…②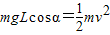 …③
…③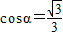 ,即:
,即: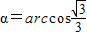 .
.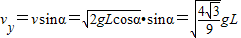 .
.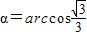 時具有最大的豎直分速度.
時具有最大的豎直分速度.

科目:高中物理 來源: 題型:
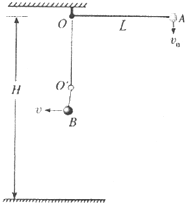 在離地面高H=2L的O點,固定一根長為L不可伸長的細輕繩,繩端系一質量為m、帶電量為+q的小球,整個空間存在豎直向下的勻強電場(圖中未畫出),電場強度E=
在離地面高H=2L的O點,固定一根長為L不可伸長的細輕繩,繩端系一質量為m、帶電量為+q的小球,整個空間存在豎直向下的勻強電場(圖中未畫出),電場強度E=| mg |
| q |
| 3L |
| 4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com