
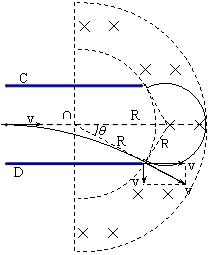
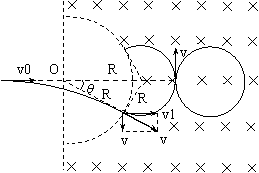
如圖甲所示,豎直放置的金屬板A、B中間開有小孔,小孔的連線沿水平放置的金屬板C、D的中間線,粒子源P可以間斷地產生質量為m、電荷量為q的帶正電粒子(初速不計),粒子在A、B間被加速后,再進入金屬板C、D間偏轉并均能從此電場中射出.已知金屬板A、B間的電壓UAB=U0,金屬板C、D長度為L,間距d= L/3.兩板之間的電壓UCD隨時間t變化的圖象如圖乙所示.在金屬板C、D右側有二個垂直紙面向里的均勻磁場分布在圖示的半環形帶中,該環帶的內、外圓心與金屬板C、D的中心O點重合,內圓半徑Rl=
L/3.兩板之間的電壓UCD隨時間t變化的圖象如圖乙所示.在金屬板C、D右側有二個垂直紙面向里的均勻磁場分布在圖示的半環形帶中,該環帶的內、外圓心與金屬板C、D的中心O點重合,內圓半徑Rl= L/3,磁感應強度B0=
L/3,磁感應強度B0= .已知粒子在偏轉電場中運動的時間遠小于電場變化的周期(電場變化的周期T未知),粒子重力不計.
.已知粒子在偏轉電場中運動的時間遠小于電場變化的周期(電場變化的周期T未知),粒子重力不計.
 (1)求粒子離開偏轉電場時,在垂直于板面方向偏移的最大距離;
(1)求粒子離開偏轉電場時,在垂直于板面方向偏移的最大距離;
(2)若所有粒子均不能從環形磁場的右側穿出,求環帶磁場的最小寬度;
(3)若原磁場無外側半圓形邊界且磁感應強度B按如圖丙所示的規律變化,設垂直紙面向里的磁場方向為正方向.t=T/2時刻進入偏轉電場的帶電微粒離開電場后進入磁場,t=3T/4時該微粒的速度方向恰好豎直向上,求該粒子在磁場中運動的時間為多少?
 解:(1)設粒子進入偏轉電場瞬間的速度為v0,
解:(1)設粒子進入偏轉電場瞬間的速度為v0,
對粒子加速過程由動能定理得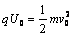
進入偏轉電場后,加速度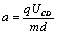
設運動時間為t,則有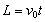
只有t=T/2時刻進入偏轉電場的粒子,垂直于極
板方向偏移的距離最大
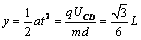
(2)t= 時刻進入偏轉電場的粒子剛好不能穿出磁場時的環帶寬度為磁場的最小寬度.
時刻進入偏轉電場的粒子剛好不能穿出磁場時的環帶寬度為磁場的最小寬度.
設粒子進入磁場時的速度為v,
對粒子的偏轉過程有 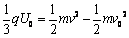 解得
解得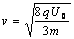
 在磁場中做圓周運動的半徑為
在磁場中做圓周運動的半徑為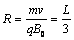
如圖所示,設環帶外圓半徑為R2,
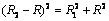
解得R2=L
所求d= R2-R1 =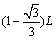
(3)微粒運動軌跡如圖所示,
微粒在磁場中做勻速圓周運動的周期為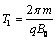
設粒子離開電場時偏轉角為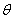 ,則
,則 解得
解得 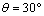
由幾何關系可知微粒運動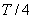 時間軌跡對應的圓心角為:
時間軌跡對應的圓心角為: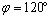
此過程微粒運動的時間為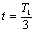
由圖可知微粒在磁場中運動的時間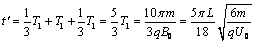


科目:高中物理 來源: 題型:
 (2009?徐匯區模擬)如圖甲所示,豎直放置的汽缸內壁光滑,活塞厚度與質量均不計,在B處設有限制裝置,使活塞只能在B以上運動,B以下汽缸的容積為V0,A、B之間的容積為0.2V0.開始時活塞在A處,溫度為87℃,大氣壓強為p0,現緩慢降低汽缸內氣體的溫度,直至活塞移動到A、B的正中間,然后保持溫度不變,在活塞上緩慢加砂,直至活塞剛好移動到B,然后再緩慢降低汽缸內氣體的溫度,直到-3℃.求:
(2009?徐匯區模擬)如圖甲所示,豎直放置的汽缸內壁光滑,活塞厚度與質量均不計,在B處設有限制裝置,使活塞只能在B以上運動,B以下汽缸的容積為V0,A、B之間的容積為0.2V0.開始時活塞在A處,溫度為87℃,大氣壓強為p0,現緩慢降低汽缸內氣體的溫度,直至活塞移動到A、B的正中間,然后保持溫度不變,在活塞上緩慢加砂,直至活塞剛好移動到B,然后再緩慢降低汽缸內氣體的溫度,直到-3℃.求:查看答案和解析>>
科目:高中物理 來源: 題型:
 (2013?松江區一模)如圖甲所示,豎直放置的無限長直導線的右側固定一小圓環,直導線與小圓環在同一平面內,導線中通入如圖乙所示電流,(規定電流方向向上時為正)下列說法正確的是( )
(2013?松江區一模)如圖甲所示,豎直放置的無限長直導線的右側固定一小圓環,直導線與小圓環在同一平面內,導線中通入如圖乙所示電流,(規定電流方向向上時為正)下列說法正確的是( )查看答案和解析>>
科目:高中物理 來源: 題型:
 如圖甲所示,豎直放置的長直導線MN通有圖示方向的恒定電流I,有一閉合矩形金屬框abcd與導線在同一平面內,在金屬框內部通有如圖乙所示的變化磁場(規定垂直于紙面向里為磁場的正方向),下列說法正確的是( )
如圖甲所示,豎直放置的長直導線MN通有圖示方向的恒定電流I,有一閉合矩形金屬框abcd與導線在同一平面內,在金屬框內部通有如圖乙所示的變化磁場(規定垂直于紙面向里為磁場的正方向),下列說法正確的是( )查看答案和解析>>
科目:高中物理 來源: 題型:
| ||
| 3 |
| ||
| 3 |
|
| T |
| 2 |
| 3T |
| 4 |
查看答案和解析>>
科目:高中物理 來源: 題型:
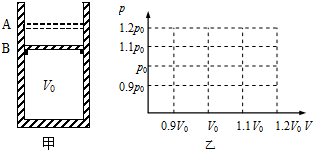 如圖甲所示,豎直放置的汽缸內壁光滑,活塞厚度與質量均不計,在B處設有限制裝置,使活塞只能在B以上運動,B以下汽缸的容積為V0,A、B之間的容積為0.2V0.開始時活塞在B處,缸內氣體的壓強與大氣壓強p0相同,溫度為77°C,現緩慢升高汽缸內氣體的溫度,直至活塞移動到A處,然后保持溫度不變,在活塞上緩慢加砂,直至活塞剛好移動到B,然后再緩慢降低汽缸內氣體的溫度,直到42°C.求:
如圖甲所示,豎直放置的汽缸內壁光滑,活塞厚度與質量均不計,在B處設有限制裝置,使活塞只能在B以上運動,B以下汽缸的容積為V0,A、B之間的容積為0.2V0.開始時活塞在B處,缸內氣體的壓強與大氣壓強p0相同,溫度為77°C,現緩慢升高汽缸內氣體的溫度,直至活塞移動到A處,然后保持溫度不變,在活塞上緩慢加砂,直至活塞剛好移動到B,然后再緩慢降低汽缸內氣體的溫度,直到42°C.求:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com