
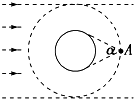
 宇宙飛船繞地球做圓周運動時,由于地球遮擋陽光,會經歷“日全食”過程,如圖所示.已知地球的半徑為R,地球質量為M,引力常量為G,地球自轉周期為T0.太陽光可看作平行光,不考慮地球公轉的影響,宇航員在A點測出地球的張角為σ,下列說法中正確的是( )
宇宙飛船繞地球做圓周運動時,由于地球遮擋陽光,會經歷“日全食”過程,如圖所示.已知地球的半徑為R,地球質量為M,引力常量為G,地球自轉周期為T0.太陽光可看作平行光,不考慮地球公轉的影響,宇航員在A點測出地球的張角為σ,下列說法中正確的是( )| A. | 飛船的高度為$\frac{R}{sin\frac{σ}{2}}$ | |
| B. | 飛船的線速度為$\sqrt{\frac{GMsin\frac{σ}{2}}{R}}$ | |
| C. | 飛船的周期為2π$\sqrt{\frac{{R}^{3}}{GMsi{n}^{3}\frac{σ}{2}}}$ | |
| D. | 飛船每次“日全食”過程的時間為$\frac{αT0}{2π}$ |
分析 宇宙飛船繞地球做勻速圓周運動,由飛船的周期及半徑可求出飛船的線速度;同時由引力提供向心力的表達式,可列出周期與半徑及角度α的關系.當飛船進入地球的影子后出現“日全食”到離開陰影后結束,所以算出在陰影里轉動的角度,即可求出發生一次“日全食”的時間.
解答 解:A、飛船繞行有:v=$\sqrt{\frac{GM}{r}}$ ①,T=2π$\sqrt{\frac{{r}^{3}}{GM}}$ ②.
應用幾何關系.在△OEA中有sin$\frac{α}{2}$=$\frac{R}{r}$ ③,飛船高度為h=r-R ④.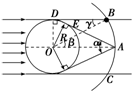
③式代入④式,解得h=R($\frac{1}{sin\frac{α}{2}}$-1),故A錯誤;
B、解①③得v=$\sqrt{\frac{GMsin\frac{σ}{2}}{R}}$,故B正確;
C、解②③得T=2π$\sqrt{\frac{{R}^{3}}{GMsi{n}^{3}\frac{σ}{2}}}$,故C正確;
D、每次“日全食”時間t為繞行BAC時間.
由△ODB≌△OEA知γ=$\frac{α}{2}$,又有β=γ,
解得β=$\frac{α}{2}$ ⑤
綜合圓周運動規律.有:2β=ωt,2π=ωT,
解得t=$\frac{Tβ}{π}$ ⑥,解⑤⑥式得t=$\frac{α}{2π}$T,故D錯誤.
故選:BC
點評 掌握勻速圓周運動中線速度、角速度及半徑的關系,同時理解萬有引力定律,并利用幾何關系得出轉動的角度.


科目:高中物理 來源: 題型:多選題
| A. | 牛頓第一定律是實驗定律,可以用實驗來驗證 | |
| B. | 牛頓第一定律表明力是改變物體運動狀態的原因 | |
| C. | 慣性定律與慣性是一回事 | |
| D. | 牛頓第一定律是牛頓第二定律的一個特例 |
查看答案和解析>>
科目:高中物理 來源: 題型:多選題
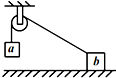 如圖,質量相同的兩物體a、b,用不可伸長的輕繩跨接在同一光滑的輕質定滑輪兩側,a在水平桌面的上方,b在水平粗糙桌面上.初始時用力壓住b使a、b靜止,撤去此壓力后,a開始運動,在a勻速下降的過程中,b始終未離開桌面.在此過程中( )
如圖,質量相同的兩物體a、b,用不可伸長的輕繩跨接在同一光滑的輕質定滑輪兩側,a在水平桌面的上方,b在水平粗糙桌面上.初始時用力壓住b使a、b靜止,撤去此壓力后,a開始運動,在a勻速下降的過程中,b始終未離開桌面.在此過程中( )| A. | b向左做勻速直線運動 | |
| B. | a、b速度大小相等 | |
| C. | a的重力勢能的減小量大于兩物體總動能的增加量 | |
| D. | b受到地面的摩擦力減小 |
查看答案和解析>>
科目:高中物理 來源: 題型:計算題
 如圖所示,定滑輪的半徑為r=10cm,繞在滑輪上的細線懸掛一重物,由靜止開始釋放,測得重物以a=2m/s2的加速度做勻加速運動.則重物由靜止開始下落至 1m 的瞬間,求:
如圖所示,定滑輪的半徑為r=10cm,繞在滑輪上的細線懸掛一重物,由靜止開始釋放,測得重物以a=2m/s2的加速度做勻加速運動.則重物由靜止開始下落至 1m 的瞬間,求:查看答案和解析>>
科目:高中物理 來源: 題型:多選題
| A. | F是物體實際受到的力 | |
| B. | F1、F2是物體實際受到的力 | |
| C. | 物體同時受到F、F1、F2三個力的作用 | |
| D. | F1、F2共同作用的效果與F相同 |
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
| A. | 單擺的振動周期與擺球質量有關 | |
| B. | 單擺經過平衡位置時所受合外力為零 | |
| C. | 將單擺從地球拿到月球時,它的周期將變小 | |
| D. | 當驅動力的頻率等于單擺的固有頻率時,單擺的振幅最大 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com