
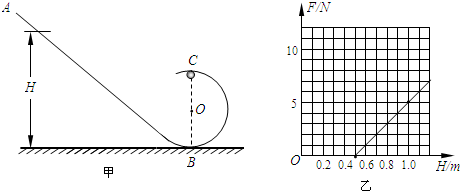
分析 (1)小球從A到C運動的過程中,只有重力做功,機械能守恒,根據機械能守恒定律和牛頓第二定律求出小球對軌道C點的壓力與H的關系式,然后結合F-H圖線求該行星表面的重力加速度.
(2)根據萬有引力提供向心力求出在圓軌道上的動能,結合初末狀態的機械能大小,通過功能關系求出火箭至少要對飛船做功的大小.
解答 解:(1)設小球質量為m,小球過C點有:$F+{m}_{C}g={m}_{C}\frac{{v}^{2}}{r}$,
對小球從出發到C點,由動能定理得,${m}_{C}g(H-2r)=\frac{1}{2}{m}_{C}{v}^{2}$,
聯立解得F=$\frac{2{m}_{C}g}{r}H-5{m}_{C}g$,
由圖可知,H1=0.5m,F1=0N,H2=1.0m,F2=5N,
解得g=5m/s2.
根據$\frac{GMm}{{R}^{2}}=mg$得,行星的質量M=$\frac{g{R}^{2}}{G}$,
代入數據解得M=1.87×1024kg.
(2)由題意可知,由于不考慮自轉,衛星在該行星表面的機械能為:${E}_{1}=-\frac{GMm}{R}$,
在h=R圓軌道上衛星的機械能:${E}_{2}=-\frac{GMm}{2R}+\frac{1}{2}m{v}^{2}$,
根據萬有引力提供向心力得:$\frac{GMm}{(2R)^{2}}=m\frac{{v}^{2}}{2R}$,
可得$\frac{1}{2}m{v}^{2}=\frac{GMm}{4R}$,
${E}_{2}=-\frac{GMm}{2R}+\frac{1}{2}m{v}^{2}=-\frac{GMm}{4R}$,
由功能關系可得,$W={E}_{2}-{E}_{1}=-\frac{GMm}{4R}-(-\frac{GMm}{R})$=$\frac{3GMm}{4R}$.
代入數據解得W=3.75×1010J.
答:(1)行星的質量為1.87×1024kg.
(2)火箭至少要對飛船做功3.75×1010J.
點評 本題是牛頓運動定律與機械能守恒定律的綜合題,解決本題的關鍵根據該規律得出壓力F與H的關系式.以及掌握萬有引力定律的兩個重要理論,并能靈活運用.


 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業安徽少年兒童出版社系列答案
暑假作業安徽少年兒童出版社系列答案科目:高中物理 來源: 題型:選擇題
| A. | 62.5m; 10 m/s | B. | 60m;10 m/s | C. | 240m;40 m/s | D. | 62.5m;40 m/s |
查看答案和解析>>
科目:高中物理 來源: 題型:解答題
 如圖所示,C為一放在固定的粗糙水平桌面上的雙斜面,其質量mC=6.5kg,頂端有一定滑輪,滑輪的質量及軸處的摩擦皆可不計,A和B是兩個滑塊,質量分別為mA=3.0kg,mB=0.50kg,由跨過定滑輪的不可伸長的輕繩相連,開始時設法抓住A、B和C,使它們都處在靜止狀態,且滑輪兩邊的輕繩恰好伸直,今用一大小等于26.5N的水平推力F作用于C,并同時釋放A、B和C,若C沿桌面向左滑行,其加速度a=3.0m/2,B相對于桌面無水平方向的位移(繩子一直是繃緊的),試求C與桌面間的μ.(圖中α=37°,β=53°,重力加速度g=10m/s2)
如圖所示,C為一放在固定的粗糙水平桌面上的雙斜面,其質量mC=6.5kg,頂端有一定滑輪,滑輪的質量及軸處的摩擦皆可不計,A和B是兩個滑塊,質量分別為mA=3.0kg,mB=0.50kg,由跨過定滑輪的不可伸長的輕繩相連,開始時設法抓住A、B和C,使它們都處在靜止狀態,且滑輪兩邊的輕繩恰好伸直,今用一大小等于26.5N的水平推力F作用于C,并同時釋放A、B和C,若C沿桌面向左滑行,其加速度a=3.0m/2,B相對于桌面無水平方向的位移(繩子一直是繃緊的),試求C與桌面間的μ.(圖中α=37°,β=53°,重力加速度g=10m/s2)查看答案和解析>>
科目:高中物理 來源: 題型:多選題
| A. | 半徑變大 | B. | 速率變大 | C. | 加速度變小 | D. | 周期變小 |
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
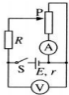
| A. | 電壓表V讀數先變大后變小,電流表A讀數變大 | |
| B. | 電壓表V讀數先變小后變大,電流表A讀數變小 | |
| C. | 電壓表V讀數先變大后變小,電流表A讀數先變小后變大 | |
| D. | 電壓表V讀數先變小后變大,電流表A讀數先變大后變小 |
查看答案和解析>>
科目:高中物理 來源: 題型:多選題
| A. | 電場用來加速帶電粒子,磁場則使帶電粒子回旋 | |
| B. | 電場和磁場同時用來加速帶電粒子 | |
| C. | 加速電壓越大,同一帶電粒子最終獲得的動能就越大 | |
| D. | 在回旋加速器的半徑一定的情況下,所加磁場越強,同一帶電粒子最終獲得的動能就越大 |
查看答案和解析>>
科目:高中物理 來源: 題型:解答題
查看答案和解析>>
科目:高中物理 來源: 題型:多選題
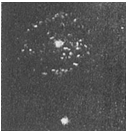 如圖為哈勃望遠鏡拍攝的銀河系中被科學家稱為“羅盤座T星”系統的照片,該系統是由一顆白矮星和它的類日伴星組成的雙星系統,圖片下面的亮點為白矮星,上面的部分為類日伴星(中央的最亮的為類似太陽的天體).由于白矮星不停地吸收由類日伴星拋出的物質致使其質量不斷增加,科學家預計這顆白矮星在不到1000萬年的時間內會完全“爆炸”,從而變成一顆超新星.現假設類日伴星所釋放的物質被白矮星全部吸收,并且兩星之間的距離在一段時間內不變,兩星球的總質量不變,不考慮其它星球對該“羅盤座T星”系統的作用,則下列說法正確的是( )
如圖為哈勃望遠鏡拍攝的銀河系中被科學家稱為“羅盤座T星”系統的照片,該系統是由一顆白矮星和它的類日伴星組成的雙星系統,圖片下面的亮點為白矮星,上面的部分為類日伴星(中央的最亮的為類似太陽的天體).由于白矮星不停地吸收由類日伴星拋出的物質致使其質量不斷增加,科學家預計這顆白矮星在不到1000萬年的時間內會完全“爆炸”,從而變成一顆超新星.現假設類日伴星所釋放的物質被白矮星全部吸收,并且兩星之間的距離在一段時間內不變,兩星球的總質量不變,不考慮其它星球對該“羅盤座T星”系統的作用,則下列說法正確的是( )| A. | 兩星之間的萬有引力不變 | B. | 兩星的運動周期不變 | ||
| C. | 類日伴星的軌道半徑減小 | D. | 白矮星的線速度變小 |
查看答案和解析>>
科目:高中物理 來源: 題型:解答題
 如圖所示,磁場中的通電導線長度為0.5m,磁感應強度為2T,通過導線的電流強度為l A,求:
如圖所示,磁場中的通電導線長度為0.5m,磁感應強度為2T,通過導線的電流強度為l A,求:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com