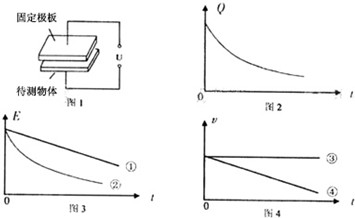
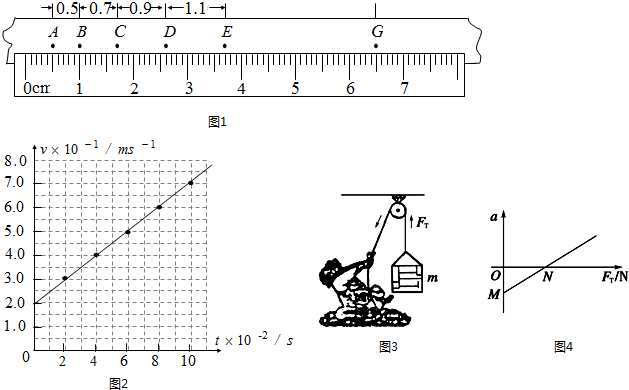
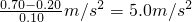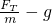解:Ⅰ①EF-DE=DE-CD,故EF=1.3cm,故F坐標值為x
F=x
E+1.3cm=3.70cm+1.3cm=5.00cm;
由平均速度等于中間時刻的瞬時速度得:
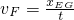
=
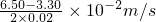
=0.70m/s
②由圖象可知,v
0=0.20m/s
斜率代表加速度,故a=
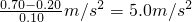
Ⅱ(1)貨物受到重力和拉力作用,根據(jù)牛頓第二定律得
F
T-mg=ma
變形得到 a=
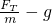
當a=0時,F(xiàn)
T=mg,即線與橫軸的交點N數(shù)值的含義為mg;
(2)由數(shù)學知識可知 a-F
T圖象是直線,其斜率等于

故答案為:(Ⅰ) ①5.00 0.70
②v
0=0.20 a=5.0
(Ⅱ) mg 貨物質量的倒數(shù)
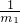
分析:Ⅰ①根據(jù)EF-DE=DE-CD可得F的坐標值;由平均速度等于中間時刻的瞬時速度求解點對應的速度大小②縱軸截距為初速度,斜率為加速度
Ⅱ(1)貨物受到重力和拉力作用,根據(jù)牛頓第二定律得到a與F
T關系表達式,運用數(shù)學知識分析截距意義(2)運用數(shù)學知識分析斜率的意義.
點評:本題考查(1)利用勻變速直線運動的規(guī)律和推論解決問題的能力,同時注意圖象法在物理實驗中的應用.(2)理解物理圖象的能力.對于圖象,往往要從物理規(guī)律進行推導,得出解析式,再應用數(shù)學知識理解其物理意義.

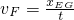 =
=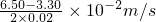 =0.70m/s
=0.70m/s