
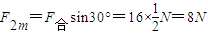 .
.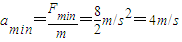 .
.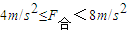 .
.

 明天教育課時特訓系列答案
明天教育課時特訓系列答案 浙江新課程三維目標測評課時特訓系列答案
浙江新課程三維目標測評課時特訓系列答案 周周清檢測系列答案
周周清檢測系列答案 輕巧奪冠周測月考直通高考系列答案
輕巧奪冠周測月考直通高考系列答案科目:高中物理 來源: 題型:
 (2010?安徽)質量為2kg的物體在水平推力F的作用下沿水平面作直線運動,一段時間后撤去F,其運動的v-t圖象如圖.g取10m/s2,求:
(2010?安徽)質量為2kg的物體在水平推力F的作用下沿水平面作直線運動,一段時間后撤去F,其運動的v-t圖象如圖.g取10m/s2,求:查看答案和解析>>
科目:高中物理 來源: 題型:
 一質量為2kg的物體在水平面上運動.在水平面內建立xoy坐標系.t=0時刻,物體處于原點位置,之后它的兩個正交分速度-時間圖象分別如圖所示.求:
一質量為2kg的物體在水平面上運動.在水平面內建立xoy坐標系.t=0時刻,物體處于原點位置,之后它的兩個正交分速度-時間圖象分別如圖所示.求:查看答案和解析>>
科目:高中物理 來源: 題型:
 如圖所示,AB與CD為兩個對稱斜面,其上部都足夠長,下部分別與一個光滑的圓弧面的兩端相切,圓弧圓心角為106°,半徑R=2.0m.一個質量為2kg的物體在離弧底E高度為h=3.0m處,以初速度v0=4m/s沿斜面向下運動,物體與兩斜面的動摩擦因數均為μ=0.2.(sin53°=0.8,sin37°=0.6,g=10m/s2)求:
如圖所示,AB與CD為兩個對稱斜面,其上部都足夠長,下部分別與一個光滑的圓弧面的兩端相切,圓弧圓心角為106°,半徑R=2.0m.一個質量為2kg的物體在離弧底E高度為h=3.0m處,以初速度v0=4m/s沿斜面向下運動,物體與兩斜面的動摩擦因數均為μ=0.2.(sin53°=0.8,sin37°=0.6,g=10m/s2)求:查看答案和解析>>
科目:高中物理 來源: 題型:
 一個質量為2kg的物體在合外力F的作用下從靜止開始運動.合外力F隨時間t變化的關系如圖示,則物體勻加速運動的加速度大小為
一個質量為2kg的物體在合外力F的作用下從靜止開始運動.合外力F隨時間t變化的關系如圖示,則物體勻加速運動的加速度大小為查看答案和解析>>
科目:高中物理 來源: 題型:

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com