
 如圖所示,區域Ⅰ、Ⅱ內存在著垂直紙面向外的勻強磁場,磁感應強度分別為B1=B,B2=0.5B.區域寬度分別為d、2d.一帶正電的粒子(重力不計)從左邊界上的A點垂直邊界射入區域Ⅰ中,粒子的質量為m,帶電量為q.
如圖所示,區域Ⅰ、Ⅱ內存在著垂直紙面向外的勻強磁場,磁感應強度分別為B1=B,B2=0.5B.區域寬度分別為d、2d.一帶正電的粒子(重力不計)從左邊界上的A點垂直邊界射入區域Ⅰ中,粒子的質量為m,帶電量為q.分析 (1)找到粒子不能進入區域II的臨界幾何條件,洛倫茲力提供向心力與幾何關系結合即可;
(2)畫出運動過程圖,找到粒子恰好能射出區域II的臨界幾何條件,再與洛倫茲力提供向心力結合即可.
解答 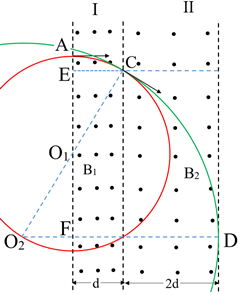
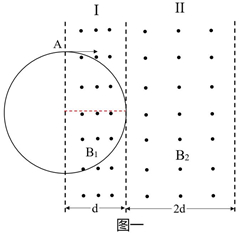 解:(1)粒子不能進入II的臨界條件為粒子軌跡恰好與I、II兩區域的邊界相切,如圖一所示
解:(1)粒子不能進入II的臨界條件為粒子軌跡恰好與I、II兩區域的邊界相切,如圖一所示
根據洛倫茲力提供向心力有:qvB1=m$\frac{{v}^{2}}{R}$ ①
粒子不能進入II區域,幾何關系應滿足:R≤d ②
聯立①②結合已知條件得:v≤$\frac{qBd}{m}$
粒子運動的周期:T=$\frac{2πR}{v}$③
聯立①③得:T=$\frac{2πm}{qB}$ ④
粒子運動的時間:t=$\frac{θ}{2π}$T ⑤
根據對稱關系可知粒子垂直入射區域I,垂直穿出區域I,所以θ=π ⑥
由④⑤⑥式聯立得t=$\frac{πm}{qB}$
(2)畫出粒子運動過程圖,如圖二所示,設粒子在區域I、II中軌跡圓的半徑分別為R1、R2,圓心分別為O1、O2,粒子在兩個區域的軌跡恰好在C點相切,又因為粒子恰好射出區域II,所以粒子在區域II中運動的軌跡與區域II的右邊界相切于D點,此時粒子恰好在D點射出區域II.
根據洛倫茲力提供向心力,在區域I中有:qvB1=m$\frac{{v}^{2}}{{R}_{1}}$ ⑦
根據洛倫茲力提供向心力,在區域II中有:qvB2=m$\frac{{v}^{2}}{{R}_{2}}$ ⑧
⑦⑧式子結合已知條件B1=B,B2=0.5B,可得:R2=2R1
根據幾何關系有:△O1EC與△O1FO2全等
可得:O2F=EC=d
所以:R2=O2D=O2F+FD=4d ⑨
⑧⑨式聯立得:v=$\frac{2qBd}{m}$
答:(1)若粒子不能進入區域Ⅱ,粒子的速度v應滿足v≤$\frac{qBd}{m}$,粒子在區域Ⅰ中運動的時間為$\frac{πm}{qB}$.
(2)若粒子剛好能射出區域Ⅱ,求粒子的速度大小為$\frac{2qBd}{m}$.
點評 本題考查帶電粒子在有界磁場中的運動,解決這類問題的思路是固定的,同學們要牢記:即洛倫茲力提供向心力與幾何關系結合;解決第二問的關鍵在于規范作圖,分析好兩軌跡在C點的速度銜接關系,兩軌跡圓恰好在C點內切.


科目:高中物理 來源: 題型:計算題

查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
| A. | 第1 s內速度的變化量小于第2 s內速度的變化量 | |
| B. | 第1 s內速度的變化量大于第2 s內速度變化量 | |
| C. | 第1 s內位移一定小于第2 s內的位移 | |
| D. | 相鄰兩段相等時間內位移之差等于一個恒量 |
查看答案和解析>>
科目:高中物理 來源: 題型:計算題
 如圖所示,離子發生器發射出一束質量為m,帶電量為q的離子(初速不計),經加速電壓u1加速后以垂直于電場方向射入兩平行板中央,受偏轉電壓u2作用后,以速度v離開電場.已知平行板的長度為L,兩板間距離為d,試證明
如圖所示,離子發生器發射出一束質量為m,帶電量為q的離子(初速不計),經加速電壓u1加速后以垂直于電場方向射入兩平行板中央,受偏轉電壓u2作用后,以速度v離開電場.已知平行板的長度為L,兩板間距離為d,試證明查看答案和解析>>
科目:高中物理 來源: 題型:計算題
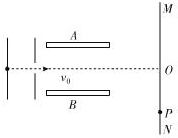 初速度為零的質子經U1=5000V的加速電壓加速后,沿著平行金屬板A、B的中心線進入平行板間的勻強電場,如圖所示,若板間距離d=1.0cm,板長l=5.0cm.距離平行金屬板s=5.0cm處有熒光屏MN,當AB間不加電壓時,質子打到熒光屏的O點.
初速度為零的質子經U1=5000V的加速電壓加速后,沿著平行金屬板A、B的中心線進入平行板間的勻強電場,如圖所示,若板間距離d=1.0cm,板長l=5.0cm.距離平行金屬板s=5.0cm處有熒光屏MN,當AB間不加電壓時,質子打到熒光屏的O點.查看答案和解析>>
科目:高中物理 來源: 題型:填空題
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
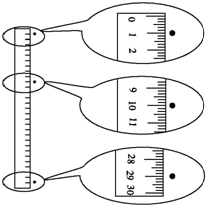 科技館里有一個展品,該展品放在暗處,頂部有一個不斷均勻向下噴射水滴的裝置,在頻閃光源的照射下,可以看到水滴好像靜止在空中固定的位置不動,如圖所示.某同學為計算該裝置噴射水滴的時間間隔,用最小刻度為毫米的刻度尺測量了空中幾滴水間的距離,由此可計算出該裝置噴射水滴的時間間隔為(g取10m/s2)( )
科技館里有一個展品,該展品放在暗處,頂部有一個不斷均勻向下噴射水滴的裝置,在頻閃光源的照射下,可以看到水滴好像靜止在空中固定的位置不動,如圖所示.某同學為計算該裝置噴射水滴的時間間隔,用最小刻度為毫米的刻度尺測量了空中幾滴水間的距離,由此可計算出該裝置噴射水滴的時間間隔為(g取10m/s2)( )| A. | 0.01 s | B. | 0.02 s | C. | 0.1 s | D. | 0.2 s |
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
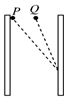 如圖所示,豎直正對放置的兩個平行金屬板間有勻強電場,在兩板之間等高處有兩個質量相同的帶電小球,P小球從緊靠左極板處靜止釋放,Q小球從兩板正中央靜止釋放,兩小球最后都打在右極板上的同一位置.則兩小球從釋放到打在右極板上的過程中( )
如圖所示,豎直正對放置的兩個平行金屬板間有勻強電場,在兩板之間等高處有兩個質量相同的帶電小球,P小球從緊靠左極板處靜止釋放,Q小球從兩板正中央靜止釋放,兩小球最后都打在右極板上的同一位置.則兩小球從釋放到打在右極板上的過程中( )| A. | 它們的運行時間tP>tQ | |
| B. | 它們的電荷量之比qP:qQ=2:1 | |
| C. | 它們的動能增加量之比△EkP:△EkQ=4:1 | |
| D. | 它們的電勢能減少量之比△EP:△EQ=4:1 |
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
 如圖所示是商場中臺階式電梯,一人靜止站在電梯水平梯板OP上,跟隨電梯以速度υ斜向上(平行NP)做勻速直線運動,下列關于水平梯板對人的支持力F和靜摩擦力f的說法,正確的是( )
如圖所示是商場中臺階式電梯,一人靜止站在電梯水平梯板OP上,跟隨電梯以速度υ斜向上(平行NP)做勻速直線運動,下列關于水平梯板對人的支持力F和靜摩擦力f的說法,正確的是( )| A. | F垂直NP斜向上 | B. | f平行NP斜向上 | C. | f平行OP向右 | D. | f=0 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com