
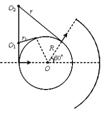
如圖甲所示,M、N為豎直放置的兩塊平行金屬板,圓形虛線為與N相連且接地的圓形金屬網罩。PQ為與圓形網罩同心的金屬收集屏,通過阻值為r0的電阻與大地相連。小孔s1、s2、圓心O與PQ中點位于同一水平線上。圓心角2θ=120°、半徑為R的網罩內有大小為B,方向垂直紙面向里的勻強磁場。M、N間相距![]() 且接有如圖乙所示的隨時間t變化的電壓,
且接有如圖乙所示的隨時間t變化的電壓,![]() (0
(0![]() t
t![]() T),
T),![]() (t >T)(式中
(t >T)(式中![]() ,T已知),質量為m、電荷量為e的質子連續不斷地經s1進入M、N間的電場,接著通過s2進入磁場。(質子通過M、N的過程中,板間電場可視為恒定,質子在s1處的速度可視為零,質子的重力及質子間相互作用均不計。)
,T已知),質量為m、電荷量為e的質子連續不斷地經s1進入M、N間的電場,接著通過s2進入磁場。(質子通過M、N的過程中,板間電場可視為恒定,質子在s1處的速度可視為零,質子的重力及質子間相互作用均不計。)
(1)質子在哪些時間段內自s1處進入板間,穿出磁場后均能打到收集屏PQ上?
(2)質子從進入s1到穿出金屬網罩經歷的時間記為![]() ,寫出
,寫出![]() 與UMN之間的函數關系(tanx=a 可表示為x=arctana)
與UMN之間的函數關系(tanx=a 可表示為x=arctana)
(3)若毎秒鐘進入s1的質子數為n,則收集屏PQ電勢穩定后的發熱功率為多少?
 |
解:
(1)質子在板間運動,根據動能定理,有![]()
![]() (1分)
(1分)
質子在磁場中運動,根據牛頓第二定律,有![]()
![]() (1分)
(1分)
若質子能打在收集屏上,軌道半徑![]() 與半徑
與半徑![]() 應滿足的關系:
應滿足的關系:![]() (1分)
(1分)
解得板間電壓![]() (1分)
(1分)
結合圖象可知:質子在![]()
![]() t
t![]()
![]() 和t
和t![]() T之間任一時刻從s1處進入電場,均能打到
T之間任一時刻從s1處進入電場,均能打到
收集屏上 (2分)
(2)M、N間的電壓越小,質子穿出電場進入磁場時的速度越小,質子在極板間經歷的時間越長,同時在磁場中運動軌跡的半徑越小,在磁場中運動的時間也會越長,設在磁場中質子運動所對應的圓半徑為r,運動圓弧所對應的圓心角為![]() ,射出電場的速度為v0,質子穿出金屬網罩時,對應總時間為t,則
,射出電場的速度為v0,質子穿出金屬網罩時,對應總時間為t,則
在板間電場中運動時間![]() (2分)
(2分)
![]()
![]() (1分)
(1分)
在磁場中運動時間![]() (1分)
(1分)
所以,運動總時間![]() =
=![]() +
+![]()
![]() (1分)
(1分)
![]() 在磁場中運動時間(1分)
在磁場中運動時間(1分)
所以,運動總時間![]() =
=![]()
![]() (2分)
(2分)
(3)穩定時, 收集屏上電荷不再增加,即在t>T 時刻以后,此時,![]() ,收集屏與地面電勢差恒為U,U=Ir0
,收集屏與地面電勢差恒為U,U=Ir0
單位時間到達收集板的質子數n
單位時間內,質子的總能量為![]() (2分)
(2分)
單位時間內屏上發熱功率為![]() (2分)
(2分)
消耗在電阻上的功率為![]() (2分)
(2分)
所以收集板發熱功率 ![]() (2分)
(2分)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中物理 來源: 題型:

查看答案和解析>>
科目:高中物理 來源: 題型:
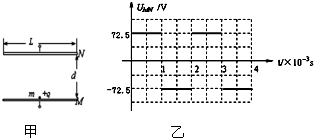 如圖甲所示,M、N為水平放置的平行板電容器的兩極板,極板長L=0.2m,兩板間距d=0.145m,在M、N間加上如圖乙所示的電壓,一個帶電粒子的電量q=+1.0×10-6C、質量m=1.0×10-8kg,粒子重力不計.
如圖甲所示,M、N為水平放置的平行板電容器的兩極板,極板長L=0.2m,兩板間距d=0.145m,在M、N間加上如圖乙所示的電壓,一個帶電粒子的電量q=+1.0×10-6C、質量m=1.0×10-8kg,粒子重力不計.查看答案和解析>>
科目:高中物理 來源: 題型:
| R |
| 2 |
| π |
| T |
| 3eB2R2 |
| m |
查看答案和解析>>
科目:高中物理 來源: 題型:
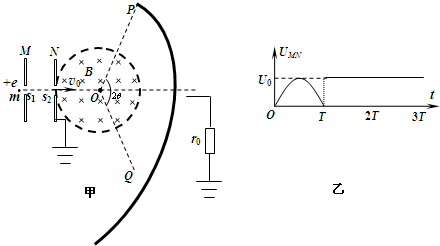
 (2012?嘉興二模)如圖甲所示,M、N為豎直放置的兩塊平行金屬板,圓形虛線為與N相連且接地的圓形金屬網罩.PQ為與圓形網罩同心的金屬收集屏,通過阻值為r0的電阻與大地相連.小孔s1、s2、圓心O與PQ中點位于同一水平線上.圓心角2θ=120°、半徑為R的網罩內有大小為B,方向垂直紙面向里的勻強磁場.M、N間相距
(2012?嘉興二模)如圖甲所示,M、N為豎直放置的兩塊平行金屬板,圓形虛線為與N相連且接地的圓形金屬網罩.PQ為與圓形網罩同心的金屬收集屏,通過阻值為r0的電阻與大地相連.小孔s1、s2、圓心O與PQ中點位于同一水平線上.圓心角2θ=120°、半徑為R的網罩內有大小為B,方向垂直紙面向里的勻強磁場.M、N間相距| R |
| 2 |
| π |
| T |
| 3eB2R2 |
| m |
查看答案和解析>>
科目:高中物理 來源: 題型:

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com