
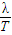 求解,故需要求出波長λ和周期T.波從A向B傳播,當A點位移達到正向最大時,B點的位移恰好為零,且向正向運動,故AB之間的距離為(n+
求解,故需要求出波長λ和周期T.波從A向B傳播,當A點位移達到正向最大時,B點的位移恰好為零,且向正向運動,故AB之間的距離為(n+ )λ,這樣求出波長λ;經0.5s(小于該波的4倍周期)后,A點位移恰好為零,且沿正向運動,而B點的位移恰好達到負的最大,故0.5s=(k+
)λ,這樣求出波長λ;經0.5s(小于該波的4倍周期)后,A點位移恰好為零,且沿正向運動,而B點的位移恰好達到負的最大,故0.5s=(k+ )T,這樣可以求出T.
)T,這樣可以求出T. )λ=6,
)λ=6, m
m )T,
)T, s,
s, s,
s,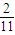 s,
s,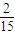 s.
s.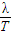 可得當λ=24m,T=
可得當λ=24m,T=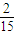 s時波速v最大,故vmax=12×15=180m/s.
s時波速v最大,故vmax=12×15=180m/s. m,T=
m,T= s時波速最小,故vmin=4m/s.
s時波速最小,故vmin=4m/s.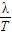 求解波速v,可以先寫出λ的一系列解和T的一系列解,最大的波速對應最大的波長和最小的周期,同理最小的波速對應最大周期和最小的波長.這是求解多解問題的基本思路.
求解波速v,可以先寫出λ的一系列解和T的一系列解,最大的波速對應最大的波長和最小的周期,同理最小的波速對應最大周期和最小的波長.這是求解多解問題的基本思路. 

 名校課堂系列答案
名校課堂系列答案科目:高中物理 來源: 題型:
查看答案和解析>>
科目:高中物理 來源: 題型:
 (1)一列簡諧波沿波的傳播方向先后有相距6m的A、B兩點,A靠近波源,且A、B間距離小于該波3倍波長.當A點位移達到正向最大時,B點的位移恰好為零,且向正向運動.經0.5s(小于該波的4倍周期)后,A點位移恰好為零,且沿正向運動,而B點的位移恰好達到負的最大.則這列波的波速:( )
(1)一列簡諧波沿波的傳播方向先后有相距6m的A、B兩點,A靠近波源,且A、B間距離小于該波3倍波長.當A點位移達到正向最大時,B點的位移恰好為零,且向正向運動.經0.5s(小于該波的4倍周期)后,A點位移恰好為零,且沿正向運動,而B點的位移恰好達到負的最大.則這列波的波速:( )| 2 |
| 3 |
查看答案和解析>>
科目:高中物理 來源:湖南模擬 題型:單選題
| A.最小值是3m/s | B.最小值是4m/s |
| C.最大值是36m/s | D.最大值是204m/s |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com