
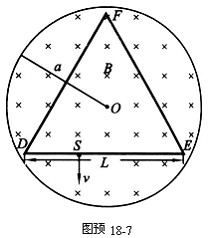
( 25分)如圖預18-7所示,在半徑為![]() 的圓柱空間中(圖中圓為其橫截面)充滿磁感應強度大小為
的圓柱空間中(圖中圓為其橫截面)充滿磁感應強度大小為![]() 的均勻磁場,其方向平行于軸線遠離讀者.在圓柱空間中垂直軸線平面內固定放置一絕緣材料制成的邊長為
的均勻磁場,其方向平行于軸線遠離讀者.在圓柱空間中垂直軸線平面內固定放置一絕緣材料制成的邊長為![]() 的剛性等邊三角形框架
的剛性等邊三角形框架![]() ,其中心
,其中心![]() 位于圓柱的軸線上.
位于圓柱的軸線上.![]() 邊上
邊上![]() 點(
點(![]() )處有一發射帶電粒子的源,發射粒子的方向皆在圖預18-7中截面內且垂直于
)處有一發射帶電粒子的源,發射粒子的方向皆在圖預18-7中截面內且垂直于![]() 邊向下.發射粒子的電量皆為
邊向下.發射粒子的電量皆為![]() (>0),質量皆為
(>0),質量皆為![]() ,但速度
,但速度![]() 有各種不同的數值.若這些粒子與三角形框架的碰撞均為完全彈性碰撞,并要求每一次碰撞時速度方向垂直于被碰的邊.試問:
有各種不同的數值.若這些粒子與三角形框架的碰撞均為完全彈性碰撞,并要求每一次碰撞時速度方向垂直于被碰的邊.試問:
1.帶電粒子速度![]() 的大小取哪些數值時可使
的大小取哪些數值時可使![]() 點發出的粒子最終又回到
點發出的粒子最終又回到![]() 點?
點?
2. 這些粒子中,回到![]() 點所用的最短時間是多少?
點所用的最短時間是多少?
參考解答
帶電粒子(以下簡稱粒子)從![]() 點垂直于
點垂直于![]() 邊以速度
邊以速度![]() 射出后,在洛倫茲力作用下做勻速圓周運動,其圓心一定位于
射出后,在洛倫茲力作用下做勻速圓周運動,其圓心一定位于![]() 邊上,其半徑
邊上,其半徑![]() 可由下式
可由下式
![]()
求得,為
![]() (1)
(1)
1. 要求此粒子每次與![]() 的三條邊碰撞時都與邊垂直,且能回到
的三條邊碰撞時都與邊垂直,且能回到![]() 點,則
點,則![]() 和
和![]() 應滿足以下條件:
應滿足以下條件:
(ⅰ)與邊垂直的條件.
由于碰撞時速度![]() 與邊垂直,粒子運動軌跡圓的圓心一定位于
與邊垂直,粒子運動軌跡圓的圓心一定位于![]() 的邊上,粒子繞過
的邊上,粒子繞過![]() 頂點
頂點![]() 、
、![]() 、
、![]() 時的圓弧的圓心就一定要在相鄰邊的交點(即
時的圓弧的圓心就一定要在相鄰邊的交點(即![]() 、
、![]() 、
、![]() )上.粒子從
)上.粒子從![]() 點開始向右作圓周運動,其軌跡為一系列半徑為
點開始向右作圓周運動,其軌跡為一系列半徑為![]() 的半圓,在
的半圓,在![]() 邊上最后一次的碰撞點與
邊上最后一次的碰撞點與![]() 點的距離應為
點的距離應為![]() ,所以
,所以![]() 的長度應是
的長度應是![]() 的奇數倍。粒子從
的奇數倍。粒子從![]() 邊繞過
邊繞過![]() 點轉回到
點轉回到![]() 點時,情況類似,即
點時,情況類似,即![]() 的長度也應是軌道半徑的奇數倍.取
的長度也應是軌道半徑的奇數倍.取![]() ,則當
,則當![]() 的長度被奇數除所得的
的長度被奇數除所得的![]() 也滿足要求,即
也滿足要求,即
![]()
![]() =1,2,3,…
=1,2,3,…
因此為使粒子與![]() 各邊發生垂直碰撞,
各邊發生垂直碰撞,![]() 必須滿足下面的條件
必須滿足下面的條件
![]() (2)
(2)
此時 ![]()
![]() 為
為![]() 的奇數倍的條件自然滿足.只要粒子繞過
的奇數倍的條件自然滿足.只要粒子繞過![]() 點與
點與![]() 邊相碰,由對稱關系可知,以后的碰撞都能與
邊相碰,由對稱關系可知,以后的碰撞都能與![]() 的邊垂直.
的邊垂直.
(ⅱ)粒子能繞過頂點與![]() 的邊相碰的條件.
的邊相碰的條件.
由于磁場局限于半徑為![]() 的圓柱范圍內,如果粒子在繞
的圓柱范圍內,如果粒子在繞![]() 點運動時圓軌跡與磁場邊界相交,它將在相交點處以此時的速度方向沿直線運動而不能返回.所以粒子作圓周運動的半徑
點運動時圓軌跡與磁場邊界相交,它將在相交點處以此時的速度方向沿直線運動而不能返回.所以粒子作圓周運動的半徑![]() 不能太大,由圖預解18-7可見,必須
不能太大,由圖預解18-7可見,必須![]() (
(![]() 的頂點沿圓柱半徑到磁場邊界的距離,
的頂點沿圓柱半徑到磁場邊界的距離,![]() 時,粒子圓運動軌跡與圓柱磁場邊界相切),由給定的數據可算得
時,粒子圓運動軌跡與圓柱磁場邊界相切),由給定的數據可算得
![]() (3)
(3)
將![]() 1,2,3,…,分別代入(2)式,得
1,2,3,…,分別代入(2)式,得
![]()
![]()
![]()
![]()
由于![]() ,
,![]() ,
,![]() ≥
≥![]() ,這些粒子在繞過
,這些粒子在繞過![]() 的頂點
的頂點![]() 時,將從磁場邊界逸出,只有
時,將從磁場邊界逸出,只有![]() ≥4的粒子能經多次碰撞繞過
≥4的粒子能經多次碰撞繞過![]() 、
、![]() 、
、![]() 點,最終回到
點,最終回到![]() 點.由此結論及(1)、(2)兩式可得與之相應的速度
點.由此結論及(1)、(2)兩式可得與之相應的速度
![]() (4)
(4)
這就是由![]() 點發出的粒子與
點發出的粒子與![]() 的三條邊垂直碰撞并最終又回到
的三條邊垂直碰撞并最終又回到![]() 點時,其速度大小必須滿足的條件
點時,其速度大小必須滿足的條件
.
2. 這些粒子在磁場中做圓周運動的周期為
![]()
將(1)式代入,得
![]() (5)
(5)
可見在![]() 及
及![]() 給定時
給定時![]() 與
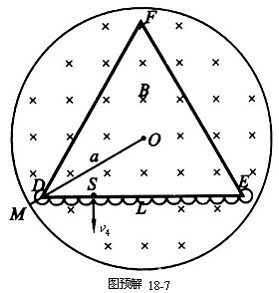
與![]() 無關。粒子從
無關。粒子從![]() 點出發最后回到
點出發最后回到![]() 點的過程中,與
點的過程中,與![]() 的邊碰撞次數愈少,所經歷的時間就愈少,所以應取
的邊碰撞次數愈少,所經歷的時間就愈少,所以應取![]() ,如圖預解18-7所示(圖中只畫出在邊框
,如圖預解18-7所示(圖中只畫出在邊框![]() 的碰撞情況),此時粒子的速度為
的碰撞情況),此時粒子的速度為![]() ,由圖可看出該粒子的軌跡包括3×13個半圓和3個圓心角為300?的圓弧,所需時間為
,由圖可看出該粒子的軌跡包括3×13個半圓和3個圓心角為300?的圓弧,所需時間為
![]() (6)
(6)
以(5)式代入得
![]() (7)
(7)


 直通貴州名校周測月考直通名校系列答案
直通貴州名校周測月考直通名校系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com