Question

（ 24分）物理小組的同學在寒冷的冬天做了一個這樣的實驗：他們把一個實心的大鋁球加熱到某溫度，然后把它放在結冰的湖面上（冰層足夠厚），鋁球便逐漸陷入冰內．當鋁球不再下陷時，測出球的最低點陷入冰中的深度．將鋁球加熱到不同的溫度，重復上述實驗8次，最終得到如下數據：

實驗順序數	1	2	3	4	5	6	7	8
熱鋁球的溫度 t /℃	55	70	85	92	104	110	120	140
陷入深度 h /cm	9.0	12.9	14.8	16.0	17.0	18.0	17.0	16.8

已知鋁的密度約為水的密度的3倍，設實驗時的環境溫度及湖面冰的溫度均為 0℃．已知此情況下，冰的熔解熱．

1．試采用以上某些數據估算鋁的比熱．

2．對未被你采用的實驗數據，試說明不采用的原因，并作出解釋．

Answer 1

六、參考解答

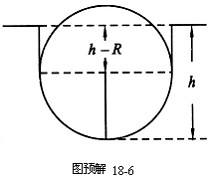
鋁球放熱，使冰熔化．設當鋁球的溫度為時，能熔化冰的最大體積恰與半個鋁球的體積相等，即鋁球的最低點下陷的深度與球的半徑相等．當熱鋁球的溫度時，鋁球最低點下陷的深度，熔化的冰的體積等于一個圓柱體的體積與半個鋁球的體積之和，如圖預解18-6-1所示．

設鋁的密度為，比熱為，冰的密度為，熔解熱為，則鋁球的溫度從℃降到0℃的過程中，放出的熱量

                           （1）

熔化的冰吸收的熱量

                                    （2）

假設不計鋁球使冰熔化過程中向外界散失的熱量，則有

                                                            （3）

解得

                                                     （4）

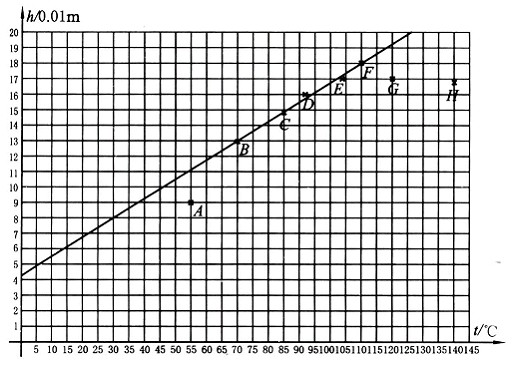
即與成線形關系．此式只對時成立。將表中數據畫在圖中，得第1，2，…，8次實驗對應的點、、…、。數據點、、、、五點可擬合成一直線，如圖預解18-6-2所示。此直線應與（4）式一致．這樣，在此直線上任取兩點的數據，代人（4）式，再解聯立方程，即可求出比熱的值．例如，在直線上取相距較遠的橫坐標為8和100的兩點和，它們的坐標由圖預解18-6-2可讀得為

                    

將此數據及的值代入（4）式，消去，得

                                                 （5）

2. 在本題作的圖預解18-6-2中，第1，7，8次實驗的數據對應的點偏離直線較遠，未被采用．這三個實驗數據在圖上的點即、、．

點為什么偏離直線較遠？因為當時，從（4）式得對應的溫度℃，（4）式在的條件才成立。但第一次實驗時鋁球的溫度℃＜，熔解的冰的體積小于半個球的體積，故（4）式不成立．

、為什么偏離直線較遠？因為鋁球的溫度過高（120℃、140℃），使得一部分冰升華成蒸氣，且因鋁球與環境的溫度相差較大而損失的熱量較多，（2）、（3）式不成立，因而（4）式不成立．

評分標準：本題24分

第1問17分；第二問7分。第一問中，（1）、（2）式各3分；（4）式4分。正確畫出圖線4分；解出（5）式再得3分。第二問中，說明、、點不采用的原因給1分；對和、偏離直線的原因解釋正確，各得3分。