
科目: 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是梯形,
是梯形,![]() ,
,![]() ,
,![]() 是正三角形,
是正三角形,![]() 為
為![]() 的中點,平面
的中點,平面![]() 平面
平面![]() .
.
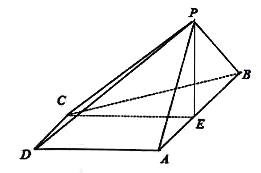
(1)求證:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在點
上是否存在點![]() ,使得二面角
,使得二面角![]() 的余弦值為
的余弦值為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】某學生為了測試煤氣灶燒水如何節省煤氣的問題設計了一個實驗,并獲得了煤氣開關旋鈕旋轉的弧度數![]() 與燒開一壺水所用時間
與燒開一壺水所用時間![]() 的一組數據,且作了一定的數據處理(如下表),得到了散點圖(如下圖).
的一組數據,且作了一定的數據處理(如下表),得到了散點圖(如下圖).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
(1)根據散點圖判斷,![]() 與
與![]() 哪一個更適宜作燒水時間
哪一個更適宜作燒水時間![]() 關于開關旋鈕旋轉的弧度數
關于開關旋鈕旋轉的弧度數![]() 的回歸方程類型?(不必說明理由)
的回歸方程類型?(不必說明理由)
(2)根據判斷結果和表中數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(3)若單位時間內煤氣輸出量![]() 與旋轉的弧度數
與旋轉的弧度數![]() 成正比,那么,利用第(2)問求得的回歸方程知
成正比,那么,利用第(2)問求得的回歸方程知![]() 為多少時,燒開一壺水最省煤氣?
為多少時,燒開一壺水最省煤氣?
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘法估計值分別為
的斜率和截距的最小二乘法估計值分別為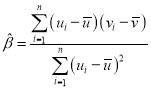 ,
,![]()
查看答案和解析>>
科目: 來源: 題型:
【題目】選修4-4:坐標系與參數方程:在平面直角坐標系![]() 中,曲線
中,曲線![]() :
:![]() (
(![]() 為參數),在以平面直角坐標系的原點為極點、
為參數),在以平面直角坐標系的原點為極點、![]() 軸的正半軸為極軸,且與平面直角坐標系
軸的正半軸為極軸,且與平面直角坐標系![]() 取相同單位長度的極坐標系中,曲線
取相同單位長度的極坐標系中,曲線![]() :
:![]() .
.
(1)求曲線![]() 的普通方程以及曲線
的普通方程以及曲線![]() 的平面直角坐標方程;
的平面直角坐標方程;
(2)若曲線![]() 上恰好存在三個不同的點到曲線
上恰好存在三個不同的點到曲線![]() 的距離相等,求這三個點的極坐標.
的距離相等,求這三個點的極坐標.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知![]() 的直角頂點
的直角頂點![]() 在
在![]() 軸上,點
軸上,點![]() 為斜邊
為斜邊![]() 的中點,且
的中點,且![]() 平行于
平行于![]() 軸.
軸.
(Ⅰ)求點![]() 的軌跡方程;
的軌跡方程;
(Ⅱ)設點![]() 的軌跡為曲線
的軌跡為曲線![]() ,直線
,直線![]() 與
與![]() 的另一個交點為
的另一個交點為![]() .以
.以![]() 為直徑的圓交
為直徑的圓交![]() 軸于
軸于![]() 即此圓的圓心為
即此圓的圓心為![]() ,
,![]() 求
求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 來源: 題型:
【題目】“搜索指數”是網民通過搜索引擎,以每天搜索關鍵詞的次數為基礎所得到的統計指標.“搜索指數”越大,表示網民對該關鍵詞的搜索次數越多,對該關鍵詞相關的信息關注度也越高.下圖是2017年9月到2018年2月這半年中,某個關鍵詞的搜索指數變化的走勢圖.

根據該走勢圖,下列結論正確的是( )
A. 這半年中,網民對該關鍵詞相關的信息關注度呈周期性變化
B. 這半年中,網民對該關鍵詞相關的信息關注度不斷減弱
C. 從網民對該關鍵詞的搜索指數來看,去年10月份的方差小于11月份的方差
D. 從網民對該關鍵詞的搜索指數來看,去年12月份的平均值大于今年1月份的平均值
查看答案和解析>>
科目: 來源: 題型:
【題目】某城市的公交公司為了方便市民出行,科學規劃車輛投放,在一個人員密集流動地段增設一個起點站,為了研究車輛發車間隔時間![]() 與乘客等候人數
與乘客等候人數![]() 之間的關系,經過調查得到如下數據:
之間的關系,經過調查得到如下數據:
間隔時間/分 | 10 | 11 | 12 | 13 | 14 | 15 |
等候人數y/人 | 23 | 25 | 26 | 29 | 28 | 31 |
調查小組先從這![]() 組數據中選取
組數據中選取![]() 組數據求線性回歸方程,再用剩下的
組數據求線性回歸方程,再用剩下的![]() 組數據進行檢驗.檢驗方法如下:先用求得的線性回歸方程計算間隔時間對應的等候人數
組數據進行檢驗.檢驗方法如下:先用求得的線性回歸方程計算間隔時間對應的等候人數![]() ,再求
,再求![]() 與實際等候人數
與實際等候人數![]() 的差,若差值的絕對值都不超過
的差,若差值的絕對值都不超過![]() ,則稱所求方程是“恰當回歸方程”.
,則稱所求方程是“恰當回歸方程”.
(1)從這![]() 組數據中隨機選取
組數據中隨機選取![]() 組數據后,求剩下的
組數據后,求剩下的![]() 組數據的間隔時間不相鄰的概率;
組數據的間隔時間不相鄰的概率;
(2)若選取的是后面![]() 組數據,求
組數據,求![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,并判斷此方程是否是“恰當回歸方程”;
,并判斷此方程是否是“恰當回歸方程”;
(3)為了使等候的乘客不超過![]() 人,試用(2)中方程估計間隔時間最多可以設置為多少(精確到整數)分鐘.
人,試用(2)中方程估計間隔時間最多可以設置為多少(精確到整數)分鐘.
附:對于一組數據![]() ,
,![]() ,……,
,……,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為:
 ,
,![]() .
.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知頂點是坐標原點的拋物線![]() 的焦點
的焦點![]() 在
在![]() 軸正半軸上,圓心在直線
軸正半軸上,圓心在直線![]() 上的圓
上的圓![]() 與
與![]() 軸相切,且
軸相切,且![]() 關于點
關于點![]() 對稱.
對稱.
(1)求![]() 和
和![]() 的標準方程;
的標準方程;
(2)過點![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() ,與
,與![]() 交于
交于![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知函數f(x)=exsinx,g(x)為f(x)的導函數,
(1)求f(x)的單調區間;
(2)當x∈[![]() ,π],證明:f(x)+g(x)(π﹣x)≥0.
,π],證明:f(x)+g(x)(π﹣x)≥0.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com