
科目: 來源: 題型:
【題目】已知![]() 表示不小于
表示不小于![]() 的最小整數,例如
的最小整數,例如![]() .
.
(1)設![]() ,
,![]() ,若
,若![]() ,求實數
,求實數![]() 的取值范圍;
的取值范圍;
(2)設![]() ,
,![]() 在區間
在區間![]()
![]() 上的值域為
上的值域為![]() ,集合
,集合![]() 中元素的個數為
中元素的個數為![]() ,求證:
,求證:![]() ;
;
(3)設![]() (
(![]() ),
),![]() ,若對于
,若對于![]() ,都有
,都有![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知無窮數列![]() 的前
的前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() ,其中
,其中![]() 、
、![]() 、
、![]() 是常數.
是常數.
(1)若![]() ,
,![]() ,
,![]() ,求數列
,求數列![]() 的通項公式;
的通項公式;
(2)若![]() ,
,![]() ,
,![]() ,且
,且![]() ,求數列
,求數列![]() 的前
的前![]() 項和
項和![]() ;
;
(3)試探究![]() 、
、![]() 、
、![]() 滿足什么條件時,數列
滿足什么條件時,數列![]() 是公比不為
是公比不為![]() 的等比數列.
的等比數列.
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖,某生態園將一三角形地塊ABC的一角APQ開辟為水果園種植桃樹,已知角A為![]() 的長度均大于200米,現在邊界AP,AQ處建圍墻,在PQ處圍竹籬笆.
的長度均大于200米,現在邊界AP,AQ處建圍墻,在PQ處圍竹籬笆.

(1)若圍墻AP,AQ總長度為200米,如何圍可使得三角形地塊APQ的面積最大?
(2)已知AP段圍墻高1米,AQ段圍墻高1.5米,造價均為每平方米100元.若圍圍墻用了20000元,問如何圍可使竹籬笆用料最省?
查看答案和解析>>
科目: 來源: 題型:
【題目】已知等差數列![]() 的首項為
的首項為![]() ,公差為
,公差為![]() ,等比數列
,等比數列![]() 的首項為
的首項為![]() ,公比為
,公比為![]() ,其中
,其中![]() ,且
,且![]() .
.
(1)求證:![]() ,并由
,并由![]() 推導
推導![]() 的值;
的值;
(2)若數列![]() 共有
共有![]() 項,前
項,前![]() 項的和為
項的和為![]() ,其后的
,其后的![]() 項的和為
項的和為![]() ,再其后的
,再其后的![]() 項的和為
項的和為![]() ,求
,求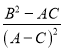 的比值.
的比值.
(3)若數列![]() 的前
的前![]() 項,前
項,前![]() 項、前
項、前![]() 項的和分別為
項的和分別為![]() ,試用含字母
,試用含字母![]() 的式子來表示
的式子來表示![]() (即
(即![]() ,且不含字母
,且不含字母![]() )
)
查看答案和解析>>
科目: 來源: 題型:
【題目】已知![]() ,
,![]() 為實數,函數
為實數,函數![]() ,且函數
,且函數![]() 是偶函數,函數
是偶函數,函數![]() 在區間
在區間![]() 上是減函數,且在區間
上是減函數,且在區間![]() 上是增函數.
上是增函數.
(1)求函數![]() 的解析式;
的解析式;
(2)求實數![]() 的值;
的值;
(3)設![]() ,問是否存在實數
,問是否存在實數![]() ,使得
,使得![]() 在區間
在區間![]() 上有最小值-2?若存在,求出
上有最小值-2?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】某電器專賣店銷售某種型號的空調,記第![]() 天(
天(![]() ,
,![]() )的日銷售量為
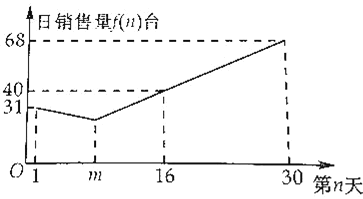
)的日銷售量為![]() (單位;臺).函數
(單位;臺).函數![]() 圖象中的點分別在兩條直線上,如圖,該兩直線交點的橫坐標為
圖象中的點分別在兩條直線上,如圖,該兩直線交點的橫坐標為![]() ,已知
,已知![]() 時,函數
時,函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的解析式;
的解析式;
(2)求![]() 的值及該店前
的值及該店前![]() 天此型號空調的銷售總量;
天此型號空調的銷售總量;
(3)按照經驗判斷,當該店此型號空調的銷售總量達到或超過![]() 臺,且日銷售量仍持續增加時,該型號空調開始旺銷,問該店此型號空調銷售到第幾天時,才可被認為開始旺銷?
臺,且日銷售量仍持續增加時,該型號空調開始旺銷,問該店此型號空調銷售到第幾天時,才可被認為開始旺銷?
查看答案和解析>>
科目: 來源: 題型:
【題目】設![]() 是數列
是數列![]() 的前
的前![]() 項和,對任意
項和,對任意![]() 都有
都有![]() 成立(其中
成立(其中![]() 是常數).
是常數).
(1)當![]() 時,求
時,求![]() :
:
(2)當![]() 時,
時,
①若![]() ,求數列
,求數列![]() 的通項公式:
的通項公式:
②設數列![]() 中任意(不同)兩項之和仍是該數列中的一項,則稱該數列是“
中任意(不同)兩項之和仍是該數列中的一項,則稱該數列是“![]() 數列”,如果
數列”,如果![]() ,試問:是否存在數列
,試問:是否存在數列![]() 為“
為“![]() 數列”,使得對任意
數列”,使得對任意![]() ,都有
,都有![]() ,且
,且![]() ,若存在,求數列
,若存在,求數列![]() 的首項
的首項![]() 的所有取值構成的集合;若不存在.說明理由.
的所有取值構成的集合;若不存在.說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知函數f(x)=x2+(x-1)|x-a|.
(1)若a=-1,解方程f(x)=1;
(2)若函數f(x)在R上單調遞增,求實數a的取值范圍;
(3)是否存在實數a,使不等式f(x)≥2x-3對任意x∈R恒成立?若存在,求出a的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】關于函數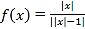 ,給出以下四個命題:(1)當
,給出以下四個命題:(1)當![]() 時,
時,![]() 單調遞減且沒有最值;(2)方程
單調遞減且沒有最值;(2)方程![]() 一定有實數解;(3)如果方程
一定有實數解;(3)如果方程![]() (
(![]() 為常數)有解,則解得個數一定是偶數;(4)
為常數)有解,則解得個數一定是偶數;(4)![]() 是偶函數且有最小值.其中假命題的序號是____________.
是偶函數且有最小值.其中假命題的序號是____________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com