
科目: 來源: 題型:
【題目】近年來,昆明加大了特色農業建設,其中花卉產業是重要組成部分.昆明斗南毗鄰滇池東岸,是著名的花都,有“全國10支鮮花7支產自斗南”之說,享有“金斗南”的美譽。對斗南花卉交易市場某個品種的玫瑰花日銷售情況進行調研,得到這種玫瑰花的定價![]() (單位:元/扎,20支/扎)和銷售率
(單位:元/扎,20支/扎)和銷售率![]() (銷售率是銷售量與供應量的比值)的統計數據如下:
(銷售率是銷售量與供應量的比值)的統計數據如下:
| 10 | 20 | 30 | 40 | 50 | 60 |
| 0.9 | 0.65 | 0.45 | 0.3 | 0.2 | 0.175 |
(1)設![]() ,根據所給參考數據判斷,回歸模型
,根據所給參考數據判斷,回歸模型![]() 與
與![]() 哪個更合適,并根據你的判斷結果求回歸方程(
哪個更合適,并根據你的判斷結果求回歸方程(![]() 、
、![]() 的結果保留一位小數);
的結果保留一位小數);
(2)某家花卉公司每天向斗南花卉交易市場提供該品種玫瑰花1200扎,根據(1)中的回歸方程,估計定價![]() (單位:元/扎)為多少時,這家公司該品種玫瑰花的日銷售額
(單位:元/扎)為多少時,這家公司該品種玫瑰花的日銷售額![]() (單位:元)最大,并求
(單位:元)最大,并求![]() 的最大值。
的最大值。
參考數據:![]() 與
與![]() 的相關系數
的相關系數![]() ,
,![]() 與
與![]() 的相關系數
的相關系數![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
參考公式: ,
,![]() ,
, .
.
查看答案和解析>>
科目: 來源: 題型:
【題目】根據中國生態環境部公布的2017年、2018年長江流域水質情況監測數據,得到如下餅圖:
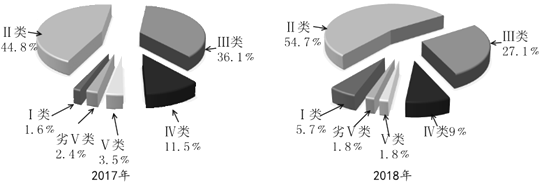
則下列說法錯誤的是( )
A.2018年的水質情況好于2017年的水質情況
B.2018年與2017年相比較,Ⅰ、Ⅱ類水質的占比明顯增加
C.2018年與2017年相比較,占比減小幅度最大的是Ⅳ類水質
D.2018年Ⅰ、Ⅱ類水質的占比超過![]()
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,底面ABCD為平行四邊形,點O為對角線BD的中點,點E,F分別為棱PC,PD的中點,已知PA⊥AB,PA⊥AD.
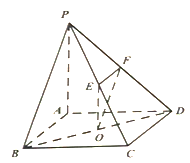
(1)求證:直線PB∥平面OEF;
(2)求證:平面OEF⊥平面ABCD.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知圓![]() 與橢圓
與橢圓![]() 相交于點M(0,1),N(0,-1),且橢圓的離心率為
相交于點M(0,1),N(0,-1),且橢圓的離心率為![]() .
.
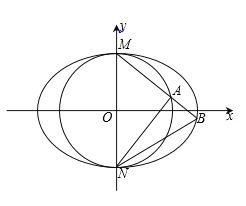
(1)求![]() 的值和橢圓C的方程;
的值和橢圓C的方程;
(2)過點M的直線![]() 交圓O和橢圓C分別于A,B兩點.
交圓O和橢圓C分別于A,B兩點.
①若![]() ,求直線
,求直線![]() 的方程;
的方程;
②設直線NA的斜率為![]() ,直線NB的斜率為
,直線NB的斜率為![]() ,問:
,問:![]() 是否為定值? 如果是,求出定值;如果不是,說明理由.
是否為定值? 如果是,求出定值;如果不是,說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知圓C經過點![]() ,且圓心
,且圓心![]() 在直線
在直線![]() 上,又直線
上,又直線![]() 與圓C交于P,Q兩點.
與圓C交于P,Q兩點.
(1)求圓C的方程;
(2)若![]() ,求實數
,求實數![]() 的值;
的值;
(3)過點![]() 作直線
作直線![]() ,且
,且![]() 交圓C于M,N兩點,求四邊形
交圓C于M,N兩點,求四邊形![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目: 來源: 題型:
【題目】2014年7月18日15時,超強臺風“威馬遜”登陸海南省.據統計,本次臺風造成全省直接經濟損失119.52億元.適逢暑假,小明調查住在自己小區的50戶居民由于臺風造成的經濟損失,作出如下頻率分布直方圖:
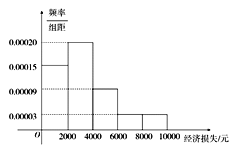
經濟損失 4000元以下 | 經濟損失 4000元以上 | 合計 | |
捐款超過500元 | 30 | ||
捐款低于500元 | 6 | ||
合計 |
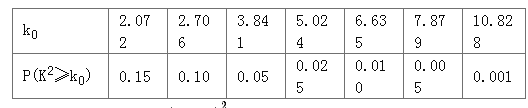
(1)臺風后區委會號召小區居民為臺風重災區捐款,小明調查的50戶居民捐款情況如上表,在表格空白處填寫正確數字,并說明是否有![]() 以上的把握認為捐款數額是否多于或少于500元和自身經濟損失是否到4000元有關?
以上的把握認為捐款數額是否多于或少于500元和自身經濟損失是否到4000元有關?
(2)臺風造成了小區多戶居民門窗損壞,若小區所有居民的門窗均由李師傅和張師傅兩人進行維修,李師傅每天早上在7:00到8:00之間的任意時刻來到小區,張師傅每天早上在7:30到8:30分之間的任意時刻來到小區,求連續3天內,李師傅比張師傅早到小區的天數的數學期望.
附:臨界值表
參考公式: ![]() .
.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知甲、乙、丙三位同學在某次考試中總成績列前三名,有![]() ,
,![]() ,
,![]() 三位學生對其排名猜測如下:
三位學生對其排名猜測如下:![]() :甲第一名,乙第二名;
:甲第一名,乙第二名;![]() :丙第一名;甲第二名;
:丙第一名;甲第二名;![]() :乙第一名,甲第三名.成績公布后得知,
:乙第一名,甲第三名.成績公布后得知,![]() ,
,![]() ,
,![]() 三人都恰好猜對了一半,則第一名是__________.
三人都恰好猜對了一半,則第一名是__________.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知函數![]() ,如果存在給定的實數對
,如果存在給定的實數對![]() ,使得
,使得![]() 恒成立,則稱
恒成立,則稱![]() 為“
為“![]() 函數”.
函數”.
(1) 判斷函數![]() 是否是“
是否是“![]() 函數”;
函數”;
(2) 若![]() 是一個“
是一個“![]() 函數”,求出所有滿足條件的有序實數對
函數”,求出所有滿足條件的有序實數對![]() ;
;
(3) 若定義域為R的函數![]() 是“
是“![]() 函數”,且存在滿足條件的有序實數對(0,1)和(1,4),當x[0,1]時,
函數”,且存在滿足條件的有序實數對(0,1)和(1,4),當x[0,1]時,![]() 的值域為[1,2],求當x[2016,2016]時函數
的值域為[1,2],求當x[2016,2016]時函數![]() 的值域.
的值域.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com