日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

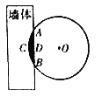
【題目】《九章算術》是我國古代數學經典名著，其中有這樣一個問題：“今有圓材，埋在壁中，不知大小.以鋸鋸之，深一寸，鋸道長一尺.問徑幾何？”其意為：今有－圓柱形木材，埋在墻壁中，不知其大小，用鋸去鋸該木材，鋸口深一寸，鋸道長－尺.問這塊圓柱形木材的直徑是多少？現有長為1丈的圓柱形木材部分鑲嵌在墻體中，截面圖如圖所示（陰影部分為鑲嵌在墻體內的部分）.已知弦尺，弓形高寸，估算該木材鑲嵌在墻體中的體積約為__________立方寸.（結果保留整數）

注：l丈＝10尺＝100寸，，.

【題目】已知橢圓的離心率為，且點在橢圓上.

（1）求橢圓的方程；

（2）若橢圓的焦點在軸上，點為坐標原點，射線、分別與橢圓交于點、點，且，試判斷直線與圓：的位置關系，并證明你的結論.

【題目】如圖，在直四棱柱中，底面是矩形，與交于點，.

（1）證明：平面；

（2）求直線與平面所成角的正弦值.

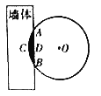
【題目】《九章算術》是我國古代數學經典名著，其中有這樣一個問題：“今有圓材，埋在壁中，不知大小.以鋸鋸之，深一寸，鋸道長一尺.問徑幾何？”其意為：今有－圓柱形木材，埋在墻壁中，不知其大小，用鋸去鋸該木材，鋸口深一寸，鋸道長－尺.問這塊圓柱形木材的直徑是多少？現有長為1丈的圓柱形木材部分鑲嵌在墻體中，截面圖如圖所示（陰影部分為鑲嵌在墻體內的部分）.已知弦尺，弓形高寸，估算該木材鑲嵌在墻體中的體積約為__________立方寸.（結果保留整數）

注：l丈＝10尺＝100寸，，.

【題目】設n為正整數，集合A=．對于集合A中的任意元素和，記

M（）=．

（Ⅰ）當n=3時，若， ，求M（）和M（）的值；

（Ⅱ）當n=4時，設B是A的子集，且滿足：對于B中的任意元素，當相同時，M（）是奇數；當不同時，M（）是偶數．求集合B中元素個數的最大值；

（Ⅲ）給定不小于2的n，設B是A的子集，且滿足：對于B中的任意兩個不同的元素，

M（）=0．寫出一個集合B，使其元素個數最多，并說明理由．

【題目】數列,定義為數列的一階差分數列,其中.

(1)若,試斷是否是等差數列,并說明理由；

(2)若證明是等差數列,并求數列的通項公式；

(3)對(2)中的數列,是否存在等差數列,使得對一切都成立,若存在,求出數列的通項公式；若不存在,請說明理由.

【題目】已知拋物線C：=2px經過點（1，2）．過點Q（0，1）的直線l與拋物線C有兩個不同的交點A，B，且直線PA交y軸于M，直線PB交y軸于N．

（Ⅰ）求直線l的斜率的取值范圍；

（Ⅱ）設O為原點，，，求證：為定值．

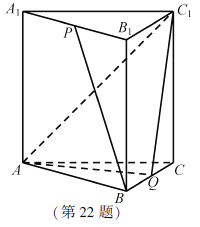
（1）求異面直線BP與AC1所成角的余弦值；

（2）求直線CC1與平面AQC1所成角的正弦值．

【題目】在實數集R中,我們定義的大小關系“＞”為全體實數排了一個“序”.類似地,我們在復數集C上也可以定義一個稱為“序”的關系,記為“＞”.定義如下:對于任意兩個復數：當且僅當“”或“”且“”.按上述定義的關系“＞”，給出以下四個命題:

①若,則；

②若，則；

③若,則對于任意；

④對于復數,若,則.

其中所有真命題的序號為______________.

規定：實心球投擲距離在之內時，測試成績為“良好”，以各組數據的中間值代表這組數據的平均值，將頻率視為概率.

（1）求，并估算該校高三年級男生實心球投擲測試成績為“良好”的百分比.

（2）現在從實心球投擲距離在，之內的男生中用分層抽樣的方法抽取5人，再從這5人中隨機抽取3人參加提高體能的訓練，求：在被抽取的3人中恰有兩人的實心球投擲距離在內的概率.