日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

設數列{a_n}滿足：a₁＝1，a_n+1＝3a_n，n∈N₊．

(Ⅰ)求{a_n}的通項公式及前n項和S_n；

(Ⅱ)已知{b_n}是等差數列，T_n為前n項和，且b₁＝a₂，b₃＝a₁＋a₂＋a₃，求T₂₀．

已知函數f(x)＝lnx，g(g)＝x²－bx(b為常數)．

(Ⅰ)函數f(x)的圖象在點(1，f(1))處的切線與函數g(x)的圖象相切，求實數b的值；

(Ⅱ)設h(x)＝f(x)＋g(x)，若函數h(x)在定義域上存在單調減區間，求實數b的取值范圍；

(Ⅲ)若b＞1，對于區間[1，2]內的任意兩個不相等的實數x₁，x₂，都有|f(x₁)－f(x₂)|＞|g(x₁)－g(x₂)|成立，求b的取值范圍．

已知橢圓的離心率為；直線l過點A(4，0)_{，B(0，2)，}且與橢圓C相切于點P．

(Ⅰ)求橢圓C的方程；

(Ⅱ)是否存在過點A(4，0)的直線m與橢圓C相交于不同的兩點M、N，使得

36|AP|²＝35|AM|·|AN|？若存在，試求出直線m的方程；若不存在，請說明理由．

如圖：在直三棱柱ABC－A₁B₁C₁中，AB＝AC＝1，∠BAC＝90°．

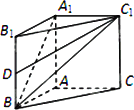
(Ⅰ)若異面直線A₁B與B₁C₁所成的角為60°，求棱柱的高h；

(Ⅱ)設D是BB₁的中點，DC₁與平面A₁BC₁所成的角為，當棱柱的高h變化時，求sin的最大值．

已知數列{a_n}的前n項和為S_n，且a₁＝，a_n+1＝S_n＋(n∈N^*，t為常數)．

(Ⅰ)若數列{a_n}為等比數列，求t的值；

(Ⅱ)若t＞－4，b_n＝lga_n+1，數列{b_n}前n項和為T_n，當且僅當n＝6時T_n取最小值，求實數t的取值范圍．

在△ABC中，內角A，B，C所對邊的邊長分別是a，b，c，已知．

(Ⅰ)若a＝2，b＝3，求△ABC的外接圓的面積；

(Ⅱ)若c＝2，sinC＋sin(B－A)＝2sin2A，求△ABC的面積．

已知拋物線C的方程為y²＝px(p＞0)，直線l：x＋y＝m與x軸的交點在拋物線C準線的右側．

(Ⅰ)求證：直線l與拋物線C恒有兩個不同交點；

(Ⅱ)已知定點A(1，0)，若直線l與拋物線C的交點為Q、R，滿足·＝0，是否存在實數m，使得原點O到直線l的距離不大于，若存在，求出正實數p的取值范圍；若不存在，請說明理由．

已知函數f(x)＝x³－ax＋1．

(Ⅰ)若x＝1時，f(x)取得極值，求a的值；

(Ⅱ)求f(x)在[0，1]上的最小值；

(Ⅲ)若對任意m∈R，直線y＝－x＋m都不是曲線y＝f(x)的切線，求a的取值范圍．

如圖所示，四棱錐P－ABCD的底面是邊長為1的正方形，PA⊥CD，PA＝1，PD＝，E為PD上一點，PE＝2ED．

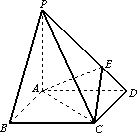
(Ⅰ)求證：PA⊥平面ABCD；

(Ⅱ)求直線PD與平面AEC所成角的正弦值；

(Ⅲ)在側棱PC上是否存在一點F，使得BF∥平面AEC？若存在，指出F點的位置，并證明；若不存在，說明理由．

數列{a_n}的前n項和，若，．

(Ⅰ)求數列{a_n}的前n項和S_n；

(Ⅱ)求數列{a_n}的通項公式；

(Ⅲ)設，求數列{b_n}的前n項和T_n．