相關習題
0 109939 109947 109953 109957 109963 109965 109969 109975 109977 109983 109989 109993 109995 109999 110005 110007 110013 110017 110019 110023 110025 110029 110031 110033 110034 110035 110037 110038 110039 110041 110043 110047 110049 110053 110055 110059 110065 110067 110073 110077 110079 110083 110089 110095 110097 110103 110107 110109 110115 110119 110125 110133 266669
科目:
來源:2007年上海市高考數學試卷(理科)(解析版)
題型:選擇題
設a,b是非零實數,若a<b,則下列不等式成立的是( )
A.a
2<b
2B.ab
2<a
2b
C.
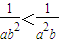
D.

查看答案和解析>>
科目:
來源:2007年上海市高考數學試卷(理科)(解析版)
題型:選擇題
在直角坐標系xOy中,

分別是與x軸,y軸平行的單位向量,若直角三角形ABC中,

,
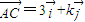
,則k的可能值有( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:
來源:2007年上海市高考數學試卷(理科)(解析版)
題型:選擇題
已知f(x)是定義域為正整數集的函數,對于定義域內任意的k,若f(k)≥k2成立,則f(k+1)≥(k+1)2成立,下列命題成立的是( )
A.若f(3)≥9成立,則對于任意k≥1,均有f(k)≥k2成立;
B.若f(4)≥16成立,則對于任意的k≥4,均有f(k)<k2成立;
C.若f(7)≥49成立,則對于任意的k<7,均有f(k)<k2成立;
D.若f(4)=25成立,則對于任意的k≥4,均有f(k)≥k2成立
查看答案和解析>>
科目:
來源:2007年上海市高考數學試卷(理科)(解析版)
題型:解答題
體積為1的直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=1,求直線AB1與平面BCC1B1所成角.
查看答案和解析>>
科目:
來源:2007年上海市高考數學試卷(理科)(解析版)
題型:解答題
在三角形ABC中,

,求三角形ABC的面積S.
查看答案和解析>>
科目:
來源:2007年上海市高考數學試卷(理科)(解析版)
題型:解答題
近年來,太陽能技術運用的步伐日益加快,已知2002年全球太陽能年生產量為670兆瓦,年增長率為34%.在此后的四年里,增長率以每年2%的速度增長(例如2003年的年生產量增長率為36%)
(1)求2006年的太陽能年生產量(精確到0.1兆瓦)
(2)已知2006年太陽能年安裝量為1420兆瓦,在此后的4年里年生產量保持42%的增長率,若2010年的年安裝量不少于年生產量的95%,求4年內年安裝量的增長率的最小值(精確到0.1%)
查看答案和解析>>
科目:
來源:2007年上海市高考數學試卷(理科)(解析版)
題型:解答題
已知函數f(x)=x
2+

(x≠0,常數a∈R).
(1)討論函數f(x)的奇偶性,并說明理由;
(2)若函數f(x)在[2,+∞)上為增函數,求實數a的取值范圍.
查看答案和解析>>
科目:
來源:2007年上海市高考數學試卷(理科)(解析版)
題型:解答題
若有窮數列a1,a2…an(n是正整數),滿足a1=an,a2=an-1…an=a1即ai=an-i+1
(i是正整數,且1≤i≤n),就稱該數列為“對稱數列”.
(1)已知數列{bn}是項數為7的對稱數列,且b1,b2,b3,b4成等差數列,b1=2,b4=11,試寫出{bn}的每一項
(2)已知{cn}是項數為2k-1(k≥1)的對稱數列,且ck,ck+1…c2k-1構成首項為50,公差為-4的等差數列,數列{cn}的前2k-1項和為S2k-1,則當k為何值時,S2k-1取到最大值?最大值為多少?
(3)對于給定的正整數m>1,試寫出所有項數不超過2m的對稱數列,使得1,2,22…2m-1成為數列中的連續項;當m>1500時,試求其中一個數列的前2008項和S2008
查看答案和解析>>
科目:
來源:2007年上海市高考數學試卷(理科)(解析版)
題型:解答題
已知半橢圓
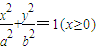
與半橢圓

組成的曲線稱為“果圓”,其中a
2=b
2+c
2,a>0,b>c>0.如圖,設點F
,F
1,F
2是相應橢圓的焦點,A
1,A
2和B
1,B
2是“果圓”與x,y軸的交點,
(1)若三角形F
F
1F
2是邊長為1的等邊三角形,求“果圓”的方程;
(2)若|A
1A|>|B
1B|,求
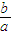
的取值范圍;
(3)一條直線與果圓交于兩點,兩點的連線段稱為果圓的弦.是否存在實數k,使得斜率為k的直線交果圓于兩點,得到的弦的中點的軌跡方程落在某個橢圓上?若存在,求出所有k的值;若不存在,說明理由.

查看答案和解析>>
科目:
來源:2010年高考數學試卷精編:10.1 排列、組合(解析版)
題型:選擇題
8名學生和2位第師站成一排合影,2位老師不相鄰的排法種數為( )
A.A88A92
B.A88C92
C.A88A72
D.A88C72
查看答案和解析>>

 分別是與x軸,y軸平行的單位向量,若直角三角形ABC中,
分別是與x軸,y軸平行的單位向量,若直角三角形ABC中, ,
,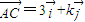 ,則k的可能值有( )
,則k的可能值有( ) (x≠0,常數a∈R).
(x≠0,常數a∈R).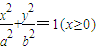 與半橢圓
與半橢圓 組成的曲線稱為“果圓”,其中a2=b2+c2,a>0,b>c>0.如圖,設點F,F1,F2是相應橢圓的焦點,A1,A2和B1,B2是“果圓”與x,y軸的交點,
組成的曲線稱為“果圓”,其中a2=b2+c2,a>0,b>c>0.如圖,設點F,F1,F2是相應橢圓的焦點,A1,A2和B1,B2是“果圓”與x,y軸的交點,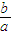 的取值范圍;
的取值范圍;