
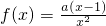 ,其中a>0.
,其中a>0.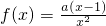 ,
,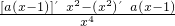 =
=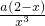
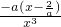 ,?x3=-ax+2,①
,?x3=-ax+2,①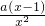 -1=0?(x2-a)(x-1)=0?x=1,x=±
-1=0?(x2-a)(x-1)=0?x=1,x=± .
. 代入①得a=1,
代入①得a=1, 代入①得a=-1,
代入①得a=-1,

 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源: 題型:
(本小題滿分14分)已知函數![]() (其中A>0,
(其中A>0,![]() )的圖象與x軸的交點中,相鄰兩個交點之間的距離為
)的圖象與x軸的交點中,相鄰兩個交點之間的距離為![]() ,且圖象上一個最低點為
,且圖象上一個最低點為![]() .(Ⅰ)求
.(Ⅰ)求![]() 的解析式;(Ⅱ)當
的解析式;(Ⅱ)當![]() ,求
,求![]() 的值域;
的值域;
查看答案和解析>>
科目:高中數學 來源:2012-2013學年山東省濟寧市汶上一中高二(下)期末數學試卷(文科)(解析版) 題型:解答題
 ,其中a>0.
,其中a>0.查看答案和解析>>
科目:高中數學 來源:2010-2011學年重慶七中高三(下)3月月考數學試卷(文科)(解析版) 題型:解答題
 ,其中a>0.
,其中a>0.查看答案和解析>>
科目:高中數學 來源:2010-2011學年湖北省武漢市武昌區高一(下)期末數學試卷(解析版) 題型:解答題
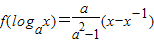 ,其中a>0且a≠1.
,其中a>0且a≠1.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com