【答案】
分析:(1)由負數沒有平方根得到1-x與x都大于等于0,列出關于x的不等式組,求出不等式組的解集即可得到函數的定義域,又因為函數為減函數,所以把x=0代入函數解析式得到函數的最大值,把x=1代入函數解析式得到函數的最小值,即可得到函數的值域;
(2)根據負數和0沒有對數得到真數x
2-2x+1大于0,即可求出x的范圍即為函數的定義域,根據x
2-2x+1大于0得到函數的值域為全體實數;
(3)根據表格得到函數的定義域為元素0,1,2,3,4,5組成的集合,值域為元素2,3,4,5,6,7組成的集合.
解答:解:(1)要使函數有意義,則
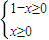
∴0≤x≤1,函數的定義域為[0,1]
∵函數y=
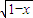
-
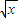
為減函數,
∴函數的值域為[-1,1].
(2)要使函數有意義,則x
2-2x+1>0,∴x≠1,
函數的定義域為{x|x≠1,x∈R}.
∵x
2-2x+1∈(0,+∞),
∴函數的值域為R.
(3)函數的定義域為{0,1,2,3,4,5},
函數的值域為{2,3,4,5,6,7}.
點評:此題考查了函數定義域及值域的求法,是一道綜合題.

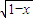 -
-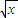 ;
;
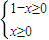
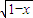 -
-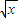 為減函數,
為減函數,

 閱讀快車系列答案
閱讀快車系列答案