
 是圓
是圓 上任意一點,點
上任意一點,點 與點
與點 關于原點對稱.線段
關于原點對稱.線段 的中垂線
的中垂線 分別與
分別與 交于
交于 兩點.
兩點. 的軌跡
的軌跡 的方程;
的方程; 與曲線
與曲線 交于
交于 兩點,若
兩點,若 (
( 為坐標原點),求直線
為坐標原點),求直線 的方程.
的方程.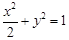 ;(2)
;(2)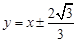
 是圓
是圓 上任意一點,點
上任意一點,點 與點
與點 關于
關于 的中垂線
的中垂線 分別與
分別與 交于
交于 兩點.利用定義法得到軌跡方程。
兩點.利用定義法得到軌跡方程。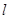 的方程為
的方程為 ,由
,由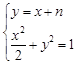 ,聯立方程組,結合韋達定理得到根與系數的關系,進一步結合向量的數量積為零得到結論。
,聯立方程組,結合韋達定理得到根與系數的關系,進一步結合向量的數量積為零得到結論。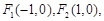 圓
圓 的半徑為
的半徑為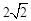 ,且
,且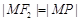 … 1分
… 1分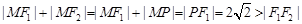 …………………………… 3分
…………………………… 3分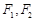 為焦點的橢圓, ………………………………………… 5分
為焦點的橢圓, ………………………………………… 5分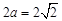 ,得到
,得到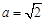 ,焦距
,焦距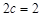 ,則短半軸
,則短半軸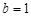
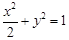 ………………………………………………………… 6分
………………………………………………………… 6分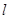 的方程為
的方程為 ,由
,由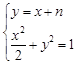
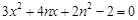 …………………………………………………………… 8分
…………………………………………………………… 8分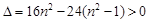 ,即
,即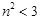 ① …………………………………9分
① …………………………………9分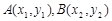 ,則
,則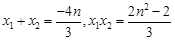
 可得
可得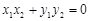 ,即
,即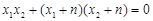 …………………10分
…………………10分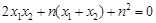
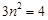 ,滿足①式,故直線
,滿足①式,故直線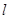 的方程為:
的方程為: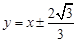 …………………12分
…………………12分

 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:高中數學 來源:不詳 題型:解答題
 ,動點N在圓
,動點N在圓 上運動,線段MN的
上運動,線段MN的 與點P的軌跡相切,且
與點P的軌跡相切,且 在
在 軸.
軸. 軸上的截距相等,求直線
軸上的截距相等,求直線 的方程.
的方程. 查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com