
(14分)已知數列![]() 的前
的前![]() 項和
項和![]() 和通項
和通項![]() 滿足
滿足![]() .
.
(Ⅰ)求數列![]() 的通項公式;
的通項公式;
(Ⅱ) 求證:![]() ;
;
(Ⅲ)設函數![]() ,
,![]() ,求
,求![]() .
.
解析:(Ⅰ)當![]() 時
時
![]() ,
,![]()
∴![]() ,---------------------------------------------------------------------------3分
,---------------------------------------------------------------------------3分
由![]() 得
得![]()
∴數列![]() 是首項
是首項![]() 、公比為
、公比為![]() 的等比數列,∴
的等比數列,∴![]() ------5分
------5分
(Ⅱ)證法1: 由![]() 得
得![]()
![]() ---------------------------------7分
---------------------------------7分
![]() ,∴
,∴![]()
∴![]() ---------------------------------------------------------9分
---------------------------------------------------------9分
〔證法2:由(Ⅰ)知![]() ,
,
∴ 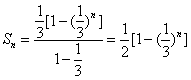 --------------------------------7分
--------------------------------7分
![]() ,∴
,∴![]() ---------------------------------8分
---------------------------------8分
即![]() -------------------------------------------------9分
-------------------------------------------------9分
(Ⅲ) ![]()
![]() =
=![]() -----------10分
-----------10分
=![]() -------------------12分
-------------------12分
∵![]()
∴![]()
![]()
![]() =
=![]() --------14分
--------14分


科目:高中數學 來源: 題型:
(本小題滿分14分)已知數列![]() 的前
的前![]() 項和
項和![]() 和通項
和通項![]() 滿足
滿足![]() (
(![]() 是常數且
是常數且![]() )。(Ⅰ)求數列
)。(Ⅰ)求數列![]() 的通項公式;(Ⅱ) 當
的通項公式;(Ⅱ) 當![]() 時,試證明
時,試證明![]() ;
;
(Ⅲ)設函數![]() ,
,![]() ,是否存在正整數
,是否存在正整數![]() ,使
,使![]() 對
對![]() 都成立?若存在,求出
都成立?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源:2011屆北京市五中高三上學期期中考試數學文卷 題型:解答題
已知數列 的前
的前 項和
項和 和通項
和通項 滿足
滿足 (
( 是常數且
是常數且 )。
)。
(Ⅰ)求數列 的通項公式;
的通項公式;
(Ⅱ) 當 時,試證明
時,試證明 ;
; (Ⅲ)設函數
(Ⅲ)設函數 ,
, ,是否存在正整數
,是否存在正整數 ,使
,使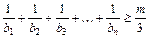 對
對 都成立?若存在,求出
都成立?若存在,求出 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年山東省濟寧市高三11月月考理科數學試卷 題型:解答題
已知數列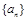 的前
的前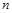 項和
項和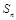 和通項
和通項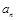 滿足
滿足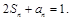 數列
數列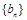 中,
中,

(1)求數列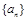 ,
,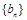 的通項公式;
的通項公式;
(2)數列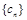 滿足
滿足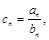 是否存在正整數
是否存在正整數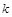 ,使得
,使得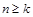 時
時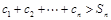 恒成立?若存在,求
恒成立?若存在,求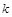 的最小值;若不存在,試說明理由.
的最小值;若不存在,試說明理由.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年北京市高三上學期期中考試數學文卷 題型:解答題
已知數列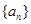 的前
的前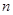 項和
項和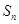 和通項
和通項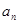 滿足
滿足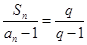 (
(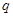 是常數且
是常數且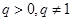 )。
)。
(Ⅰ)求數列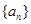 的通項公式;
的通項公式;
(Ⅱ) 當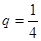 時,試證明
時,試證明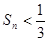 ;
;
(Ⅲ)設函數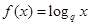 ,
, ,是否存在正整數
,是否存在正整數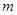 ,使
,使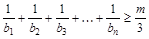 對
對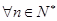 都成立?若存在,求出
都成立?若存在,求出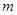 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com