
如圖,將邊長為2的正方形ABCD沿對角線BD折疊,使的平面ABD⊥平面CBD,AE⊥平面ABD,且AE=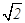 ,
,

(1) 求證:DE⊥AC
(2)求DE與平面BEC所成角的正弦值
(3)直線BE上是否存在一點M,使得CM//平面ADE,若存在,求M的位置,不存在,請說明理由。
(1)以A為原點,以射線AB,AC,AE為坐標軸建立空間直角坐標系,
則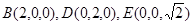 由C作平面ABD的垂線,垂足為F,則F為BC的中點,
由C作平面ABD的垂線,垂足為F,則F為BC的中點,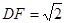 ,所以點C的坐標為
,所以點C的坐標為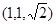 ,
,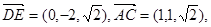
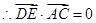
故:DE⊥AC(2)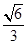 (3)存在M為BE的中點,使得CM//平面ADE
(3)存在M為BE的中點,使得CM//平面ADE
【解析】
試題分析:以A為原點,以射線AB,AC,AE為坐標軸建立空間直角坐標系,
則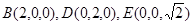
由C作平面ABD的垂線,垂足為F,則F為BC的中點,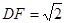 ,
,
所以點C的坐標為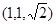 。
。
(1)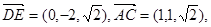
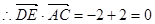 ,故:DE⊥AC。
,故:DE⊥AC。
(2)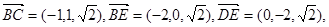
設平面BCE的法向量為 ,則
,則 ,
,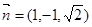
設線面角為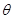 ,
,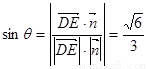
(3)設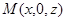 ,則
,則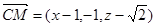 。若CM//平面ADE,則
。若CM//平面ADE,則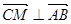 ,所以
,所以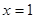 ,故存在M為BE的中點,使得CM//平面ADE。
,故存在M為BE的中點,使得CM//平面ADE。
考點:空間線面平行的判定及性質,線面所成角的求解
點評:采用空間向量的方法求解立體幾何問題的步驟:建立空間直角坐標系,寫出相關點及相關向量的坐標,將坐標代入證明或計算求解的對應公式求解,空間向量法要求學生數據處理時認真仔細


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
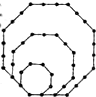 (2012•蕪湖三模)如圖,將邊長為1,2,3的正八邊形疊放在一起,同一邊上相鄰珠子的距離為1,若以此方式再放置邊長為4,5,6,…,10的正八邊形,則這10個正八邊形鑲嵌的珠子總數是
(2012•蕪湖三模)如圖,將邊長為1,2,3的正八邊形疊放在一起,同一邊上相鄰珠子的距離為1,若以此方式再放置邊長為4,5,6,…,10的正八邊形,則這10個正八邊形鑲嵌的珠子總數是查看答案和解析>>
科目:高中數學 來源: 題型:
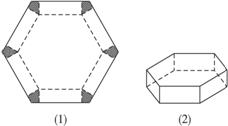
09年湖北鄂州5月模擬文)(12分)如圖所示,將邊長為2的正三角形鐵皮的三個角各切去一個全等的四邊形,再沿虛線折起,做成一個無蓋的正三棱柱容器,要求正三棱柱容器的高x與底面邊長之比不超過正常數t.
⑴把正三棱柱容器的容積V表示為x的函數,并寫出函數的定義域;
⑵x為何值時,容積V最大?并求最大值.

查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:2010-2011年福建省高二第二學期導數及其運用數學理卷 題型:填空題
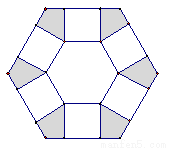
如圖,將邊長為2的正六邊形鐵皮的六個角各剪去一個全等四邊形,再折起做一個無蓋正六棱柱容器,其容積最大時,底面邊長為.
查看答案和解析>>
科目:高中數學 來源: 題型:
![]()
圖1 圖2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com