【答案】
分析:此題關鍵在于分類討論,注意x>0的前提,討論x的值,去絕對值,根據判別式進行判定根的個數.
解答:解:方程兩邊平方|1-x|=(kx)
2,并且由原方程還得出x>0
①x=1,左邊=0,右邊由于k≠0所以不為零.所以x=1不是解.
②x>1,去絕對值符號:x-1=k
2x
2即k
2x
2-x+1=0
判別式△=1-4k
2由于

,故△∈(0,1)所以有兩個解.
當然還需要判斷這兩個解是不是都大于1的.的確,這是顯然的,因為方程x-1=k2x2右邊一定大于0,故兩解一定是大于1的.
③x<1,去絕對值符號:1-x=k
2x
2即k
2x
2+x-1=0判別式△=1+4k
2>0所以有兩個解.
同樣,因為方程1-x=k
2x
2右邊一定大于0,故兩解一定是小于1的.但是,還需要判斷這兩個解是否都大于零.
由根與系數的關系:兩根之積:-
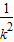
<0這就說明兩根一正一負!那個負根是不能要的,所以舍去總共3個解
故選D.
點評:本題主要考查了函數與方程的綜合運用,以及分類討論的思想,解題時需注意前提條件,需要細心研究,屬于中檔題.

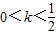 時,方程
時,方程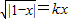 的解的個數是( )
的解的個數是( ) ,故△∈(0,1)所以有兩個解.
,故△∈(0,1)所以有兩個解.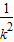 <0這就說明兩根一正一負!那個負根是不能要的,所以舍去總共3個解
<0這就說明兩根一正一負!那個負根是不能要的,所以舍去總共3個解

 名校課堂系列答案
名校課堂系列答案