【題目】已知
, 
.
(1)當
時， 
為增函數(shù)，求實數(shù)
的取值范圍；
(2)設函數(shù)
，若不等式
對
恒成立，求實數(shù)
的取值范圍.
【答案】（1）
（2）
【解析】試題分析：（1）作差，求導，利用導函數(shù)非負恒成立轉化為不等式恒成立問題，再分離參數(shù)，將問題轉化為利用導數(shù)研究函數(shù)的最值問題；（2）作差構造函數(shù)，求導，利用導函數(shù)的符號變換確定導數(shù)的單調性和最值.
試題解析：（1）∵
，∴
.
∵
時
為增函數(shù)，∴
對
恒成立，即
.
令
, 
,則
，令
解得
.
∴
在
單減； 
單增，∵
，
，∴
.
（2）∵
對
恒成立，令
得
，
令
，則
，
，則
，
令
，則
，
則
在
單增， 
單減； 
，故
對
恒成立.
∴
在
單減，∵
，無論
在
有無零點，
在
上的最小值只可能為
或
，
要
恒成立，∴
且
，∴
.
法二： 
，即
，令
， 
，
令
得
，∴
在
單增； 
單減，
又∵
有唯一零點
，所以可作出函數(shù)
的示意圖，
要滿足
對
恒成立，只需
解得
.
科目：高中數(shù)學 來源： 題型：
【題目】在扶貧活動中，為了盡快脫貧(無債務)致富，企業(yè)甲將經營狀況良好的某種消費品專賣店以5.8萬元的優(yōu)惠價格轉讓給了尚有5萬元無息貸款沒有償還的小型企業(yè)乙，并約定從該店經營的利潤中，首先保證企業(yè)乙的全體職工每月最低生活費的開支3 600元后，逐步償還轉讓費(不計息)．在甲提供的資料中：①這種消費品的進價為每件14元；②該店月銷量Q(百件)與銷量價格P(元)的關系如圖所示；③每月需各種開支2 000元．
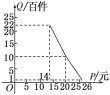
(1)當商品的價格為每件多少元時，月利潤扣除職工最低生活費的余額最大？并求最大余額；
(2)企業(yè)乙只依靠該店，最早可望在幾年后脫貧？
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知向量
，向量
，函數(shù)
.
（I）求
單調遞減區(qū)間；
（II）已知
分別為
內角
的對邊，
為銳角，
，且
恰是在
上的最大值，求
和的面積
.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，在四棱錐P—ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中點.
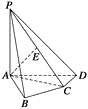
(1) 證明：AE⊥平面PCD；
(2) 求PB和平面PAD所成的角的大小.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)f(x)＝x2＋bx為偶函數(shù)，數(shù)列{an}滿足an＋1＝2f(an－1)＋1，且a1＝3，an>1.
(1)設bn＝log2(an－1)，證明：數(shù)列{bn＋1}為等比數(shù)列；
(2)設cn＝nbn，求數(shù)列{cn}的前n項和Sn.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，在四棱錐PABCD中，側面PAB⊥底面ABCD，底面ABCD為矩形，PA＝PB，O為AB的中點，OD⊥PC.
(1)求證：OC⊥PD；
(2)若PD與平面PAB所成的角為30°，求二面角DPCB的余弦值．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知點P(2，2)，圓C：x2＋y2－8y＝0，過點P的動直線l與圓C交于A，B兩點，線段AB的中點為M，O為坐標原點．
(1)求M的軌跡方程；
(2)當|OP|＝|OM|時，求l的方程及△POM的面積．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知動點P到定點F(1，0)和到直線x＝2的距離之比為
，設動點P的軌跡為曲線E，過點F作垂直于x軸的直線與曲線E相交于A，B兩點，直線l：y＝mx＋n與曲線E交于C，D兩點，與線段AB相交于一點(與A，B不重合)．
(1)求曲線E的方程；
(2)當直線l與圓x2＋y2＝1相切時，四邊形ABCD的面積是否有最大值？若有，求出其最大值及對應的直線l的方程；若沒有，請說明理由．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知二次函數(shù)f(x)＝x2＋ax＋b(a，b∈R)的定義域為[－1，1]，且|f(x)|的最大值為M.
(1)證明：|1＋b|≤M；
(2)證明：M≥
.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com