
【題目】
【答案】(1)![]() ,極小值為
,極小值為![]() 無極大值;(2)見解析;(3)見解析.
無極大值;(2)見解析;(3)見解析.
【解析】試題分析:(1)求導,由![]() ,由導數工具求得極值;(2)令,
,由導數工具求得極值;(2)令, ![]() ;(3)解法一:①若
;(3)解法一:①若![]() ,由(2)得,存在
,由(2)得,存在![]() 使得命題恒成立.②若
使得命題恒成立.②若![]() ,令
,令![]() ,命題轉化為
,命題轉化為![]() 成立,即只要
成立,即只要![]() 成立.令
成立.令![]() ,利用導數工具得:取
,利用導數工具得:取![]() ,
, ![]() .即存在
.即存在![]() ,使得原命題成立. 解法二:對任意給定的正數c,取
,使得原命題成立. 解法二:對任意給定的正數c,取![]() 由(2)知,當x>0時,
由(2)知,當x>0時, ![]()
![]() 當
當![]() 時,
時, ![]()
![]()
![]() ,故對任意給定的正數c,總存在
,故對任意給定的正數c,總存在![]() ,當
,當![]() 時,恒有
時,恒有![]() .
.
試題解析:
(1)由![]() ,得
,得![]() .又
.又![]() ,得
,得![]() .所以
.所以
![]() .令
.令![]() ,得
,得![]() .當
.當![]() 時,
時, ![]() 單
單
調遞減;當![]() 時,
時, ![]() 單調遞增.所以當
單調遞增.所以當![]() 時,
時, ![]() 取得極小值,且極
取得極小值,且極
小值為![]() 無極大值.
無極大值.
(2)令![]() ,則
,則![]() .由(I)得
.由(I)得![]() ,故
,故![]() 在R上單調遞增,又
在R上單調遞增,又![]() ,因此,當
,因此,當![]() 時,
時, ![]() ,即
,即![]() ,
,
(3)解法一:①若![]() ,則
,則![]() .又由(II)知,當
.又由(II)知,當![]() 時,
時, ![]() .所以當
.所以當![]() 時,
時, ![]() .取
.取![]() ,當
,當![]() 時,恒有
時,恒有![]() .
.
②若![]() ,令
,令![]() ,要使不等式
,要使不等式![]() 成立,只要
成立,只要![]() 成立.而要使
成立.而要使![]() 成立,則只要
成立,則只要![]() ,只要
,只要![]() 成立.令
成立.令![]() ,則
,則![]() .所以當
.所以當![]() 時,
時, ![]() 在
在![]() 內單調遞增.取
內單調遞增.取![]() ,所以
,所以![]() 在
在![]() 內單調遞增.又
內單調遞增.又![]() .易知
.易知![]() .所以
.所以![]() .即存在
.即存在![]() ,當
,當![]() 時,恒有
時,恒有![]() .
.
綜上,對任意給定的正數c,總存在![]() ,當
,當![]() 時,恒有
時,恒有![]() .
.
解法二:對任意給定的正數c,取![]()
由(2)知,當x>0時, ![]() ,所以
,所以![]()
當![]() 時,
時, ![]()
因此,對任意給定的正數c,總存在![]() ,當
,當![]() 時,恒有
時,恒有![]() .
.


科目:高中數學 來源: 題型:
【題目】有一種新型的洗衣液,去污速度特別快.已知每投放k(1≤k≤4,且k∈R)個單位的洗衣液在一定量水的洗衣機中,它在水中釋放的濃度y(克/升)隨著時間x(分鐘)變化的函數關系式近似為y=k·f(x),其中f(x)=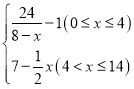 若多次投放,則某一時刻水中的洗衣液濃度為每次投放的洗衣液在相應時刻所釋放的濃度之和.根據經驗,當水中洗衣液的濃度不低于4(克/升)時,它才能起到有效去污的作用.
若多次投放,則某一時刻水中的洗衣液濃度為每次投放的洗衣液在相應時刻所釋放的濃度之和.根據經驗,當水中洗衣液的濃度不低于4(克/升)時,它才能起到有效去污的作用.
(1)若只投放一次k個單位的洗衣液,兩分鐘時水中洗衣液的濃度為3(克/升),求k的值;
(2)若只投放一次4個單位的洗衣液,則有效去污時間可達幾分鐘?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=2sin(x-![]() )-
)-![]() ,現將f(x)的圖象向左平移
,現將f(x)的圖象向左平移![]() 個單位長度,再向上平移
個單位長度,再向上平移![]() 個單位長度,得到函數g(x)的圖象.
個單位長度,得到函數g(x)的圖象.
(1)求f(![]() )+g(
)+g(![]() )的值;
)的值;
(2)若a,b,c分別是△ABC三個內角A,B,C的對邊,a+c=4,且當x=B時,g(x)取得最大值,求b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
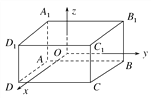
【題目】如圖,已知長方體ABCD-A1B1C1D1的對稱中心在坐標原點,交于同一頂點的三個面分別平行于三個坐標平面,頂點A(-2,-3,-1),求其他七個頂點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C:x2+y2-8y+12=0,直線l經過點D(-2,0),且斜率為k.
(1)求以線段CD為直徑的圓E的方程.
(2)若直線l與圓C相離,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一臺機器按不同的轉速生產出來的某機械零件有一些會有缺點,每小時生產有缺點的零件的多少隨機器的運轉的速度的變化而變化,下表為抽樣試驗的結果:
轉速 | 16 | 14 | 12 | 8 |
每小時生產有缺點的零件數 | 11 | 9 | 8 | 5 |
(1)畫出散點圖;
(2)如果![]() 對
對![]() 有線性相關關系,請畫出一條直線近似地表示這種線性關系;
有線性相關關系,請畫出一條直線近似地表示這種線性關系;
(3)在實際生產中,若它們的近似方程為![]() ,允許每小時生產的產品中有缺點的零件最多為
,允許每小時生產的產品中有缺點的零件最多為![]() 件,那么機器的運轉速度應控制在什么范圍內?
件,那么機器的運轉速度應控制在什么范圍內?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com