
【題目】設F1,F2分別為橢圓C![]()
(1)若橢圓C上的點![]()
(2)設點K是(1)中所得橢圓上的動點,求線段F1K的中點的軌跡方程;
(3)已知橢圓具有性質:若M,N是橢圓C上關于原點對稱的兩個點,點P是橢圓上任意一點,當直線PM,PN的斜率都存在,并記為kPM,kPN時,那么kPM與kPN之積是與點P位置無關的定值,試寫出雙曲![]()
【答案】(1)見解析;(2)![]() ;(3)見解析
;(3)見解析
【解析】
分析:(1)到兩交點的距離之和為4,點![]() 在曲線上,列出
在曲線上,列出![]() 的方程求解即可。
的方程求解即可。
(2)設橢圓![]() 上的動點為
上的動點為![]() ,線段
,線段![]() 的中點
的中點![]() ,利用中點的坐標關系式,列出
,利用中點的坐標關系式,列出![]() 與
與![]() 的坐標關系,用
的坐標關系,用![]() 表示出
表示出![]() ,代入橢圓方程即可。
,代入橢圓方程即可。
(3)分別設出![]() 的坐標,表示出斜率
的坐標,表示出斜率![]() 化簡整理即可。
化簡整理即可。
詳解:(1)橢圓C的焦點在x軸上.由橢圓上的點A到F1,F2兩點的距離之和是4,得2a=4,即a=2.
又點A![]() ,
,
∴![]() +
+![]() =1,b2=3.
=1,b2=3.
∴c2=a2-b2=1.
∴橢圓C的方程![]() +
+![]() =1,焦點F1(-1,0),F2(1,0).
=1,焦點F1(-1,0),F2(1,0).
(2)設橢圓C上的動點為K(x1,y1),線段F1K的中點Q(x,y)滿足:x=![]() ,y=
,y=![]() ,
,
∴x1=2x+1,y1=2y.
∴![]() +
+![]() =1,
=1,
![]() +
+![]() =1為所求的軌跡方程.
=1為所求的軌跡方程.
(3)類似的性質為:若M,N是雙曲![]() -
-![]() =1(a>0,b>0)上關于原點對稱的兩個點,點P是雙曲線上任意一點,當直線PM,PN的斜率都存在,并記為kPM,kPN時,那么kPM與kPN之積是與點P位置無關的定值.
=1(a>0,b>0)上關于原點對稱的兩個點,點P是雙曲線上任意一點,當直線PM,PN的斜率都存在,并記為kPM,kPN時,那么kPM與kPN之積是與點P位置無關的定值.
證明:設點M的坐標為(m,n),則點N的坐標為(-m,-n),其![]() -
-![]() =1.
=1.
又設點P的坐標為(x,y),
∵kPM=![]() ,kPN=
,kPN=![]() ,
,
∴kPM·kPN=![]() .
.
![]() -
-![]() =1,
=1,
∴x2=![]() a2,m2=
a2,m2=![]() a2.
a2.
∴x2-m2=![]() (y2-n2).
(y2-n2).
∴kPM·kPN=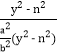 =
=![]() (定值).
(定值).


科目:高中數學 來源: 題型:
【題目】
(1)[選修4﹣1:幾何證明選講]
如圖,AB是圓O的直徑,D,E為圓上位于AB異側的兩點,連接BD并延長至點C,使BD=DC,連接AC,AE,DE.
求證:∠E=∠C.
(2)[選修4﹣2:矩陣與變換]
已知矩陣A的逆矩陣  ,求矩陣A的特征值.
,求矩陣A的特征值.
(3)[選修4﹣4:坐標系與參數方程]
在極坐標中,已知圓C經過點P( ![]() ,
, ![]() ),圓心為直線ρsin(θ﹣
),圓心為直線ρsin(θ﹣ ![]() )=﹣
)=﹣ ![]() 與極軸的交點,求圓C的極坐標方程.
與極軸的交點,求圓C的極坐標方程.
(4)[選修4﹣5:不等式選講]
已知實數x,y滿足:|x+y|< ![]() ,|2x﹣y|<
,|2x﹣y|< ![]() ,求證:|y|<
,求證:|y|< ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】北京某附屬中學為了改善學生的住宿條件,決定在學校附近修建學生宿舍,學校總務辦公室用1000萬元從政府購得一塊廉價土地,該土地可以建造每層1000平方米的樓房,樓房的每平方米建筑費用與建筑高度有關,樓房每升高一層,整層樓每平方米建筑費用提高0.02萬元,已知建筑第5層樓房時,每平方米建筑費用為0.8萬元.
(1)若學生宿舍建筑為![]() 層樓時,該樓房綜合費用為
層樓時,該樓房綜合費用為![]() 萬元,綜合費用是建筑費用與購地費用之和),寫出
萬元,綜合費用是建筑費用與購地費用之和),寫出![]() 的表達式;
的表達式;
(2)為了使該樓房每平方米的平均綜合費用最低,學校應把樓層建成幾層?此時平均綜合費用為每平方米多少萬元?
【答案】(1)![]() ;(2)學校應把樓層建成
;(2)學校應把樓層建成![]() 層,此時平均綜合費用為每平方米
層,此時平均綜合費用為每平方米![]() 萬元
萬元
【解析】
![]() 由已知求出第
由已知求出第![]() 層樓房每平方米建筑費用為
層樓房每平方米建筑費用為![]() 萬元,得到第
萬元,得到第![]() 層樓房建筑費用,由樓房每升高一層,整層樓建筑費用提高
層樓房建筑費用,由樓房每升高一層,整層樓建筑費用提高![]() 萬元
萬元![]() ,然后利用等差數列前
,然后利用等差數列前![]() 項和求建筑
項和求建筑![]() 層樓時的綜合費用
層樓時的綜合費用![]() ;
;
![]() 設樓房每平方米的平均綜合費用為
設樓房每平方米的平均綜合費用為![]() ,則
,則![]() ,然后利用基本不等式求最值.
,然后利用基本不等式求最值.
解:![]() 由建筑第5層樓房時,每平方米建筑費用為
由建筑第5層樓房時,每平方米建筑費用為![]() 萬元,
萬元,
且樓房每升高一層,整層樓每平方米建筑費用提高![]() 萬元,
萬元,
可得建筑第1層樓房每平方米建筑費用為:![]() 萬元.
萬元.
建筑第1層樓房建筑費用為:![]() 萬元
萬元![]() .
.
樓房每升高一層,整層樓建筑費用提高:![]() 萬元
萬元![]() .
.
建筑第x層樓時,該樓房綜合費用為:![]() .
.
![]() ;
;
![]() 設該樓房每平方米的平均綜合費用為
設該樓房每平方米的平均綜合費用為![]() ,
,
則:![]() ,
,
當且僅當![]() ,即
,即![]() 時,上式等號成立.
時,上式等號成立.
![]() 學校應把樓層建成10層,此時平均綜合費用為每平方米
學校應把樓層建成10層,此時平均綜合費用為每平方米![]() 萬元.
萬元.
【點睛】
本題考查簡單的數學建模思想方法,訓練了等差數列前n項和的求法,訓練了利用基本不等式求最值,是中檔題.
【題型】解答題
【結束】
20
【題目】已知![]() .
.
(1)求函數![]() 的最小正周期和對稱軸方程;
的最小正周期和對稱軸方程;
(2)若![]() ,求
,求![]() 的值域.
的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有0,1,2,3,4,5六個數字.
(1)用所給數字能夠組成多少個四位數?
(2)用所給數字可以組成多少個沒有重復數字的五位數?
(3)用所給數字可以組成多少個沒有重復數字且比3142大的數?(最后結果均用數字作答)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2015·新課標1卷)已知橢圓E的中心為坐標原點,離心率為![]() , E的右焦點與拋物線C:y2=8x的焦點重合,A,B是C的準線與E的兩個交點,則|AB|= ( )
, E的右焦點與拋物線C:y2=8x的焦點重合,A,B是C的準線與E的兩個交點,則|AB|= ( )
A.3
B.6
C.9
D.12
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知O為坐標原點,F是橢圓C: ![]() =1(a>b>0)的左焦點,A,B分別為C的左,右頂點.P為C上一點,且PF⊥x軸,過點A的直線l與線段PF交于點M,與y軸交于點E.若直線BM經過OE的中點,則C的離心率為( )
=1(a>b>0)的左焦點,A,B分別為C的左,右頂點.P為C上一點,且PF⊥x軸,過點A的直線l與線段PF交于點M,與y軸交于點E.若直線BM經過OE的中點,則C的離心率為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某服裝店為慶祝開業“三周年”,舉行為期六天的促銷活動,規定消費達到一定標準的顧客可進行一次抽獎活動,隨著抽獎活動的有效開展,第五天該服裝店經理對前五天中參加抽獎活動的人數進行統計,![]() 表示第
表示第![]() 天參加抽獎活動的人數,得到統計表格如下:
天參加抽獎活動的人數,得到統計表格如下:
| 1 | 2 | 3 | 4 | 5 |
| 4 | 6 | 10 | 23 | 22 |
(1)若![]() 與
與![]() 具有線性相關關系,請根據上表提供的數據,用最小二乘法求出
具有線性相關關系,請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)預測第六天的參加抽獎活動的人數(按四舍五入取到整數).
參考公式與參考數據: .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四棱錐P - ABCD的底面為直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC![]()
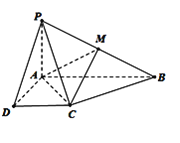
(1)證明平面PAD⊥平面PCD;
(2)求AC與PB所成角的余弦值;
(3)求平面AMC與平面BMC所成二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1. 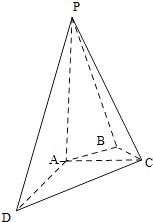
(1)證明:PC⊥AD;
(2)求二面角A﹣PC﹣D的正弦值;
(3)設E為棱PA上的點,滿足異面直線BE與CD所成的角為30°,求AE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com