
【題目】據某氣象中心觀察和預測:發生于M地的沙塵暴一直向正南方向移動,其移動速度v(km/h)與時間t(h)的函數圖象如圖所示.過線段OC上一點T(t,0)作橫軸的垂線l,梯形OABC在直線l左側部分的面積即時間t(h)內沙塵暴所經過的路程s(km).

(1)當t=4時,求s的值;
(2)將s隨t變化的規律用數學關系式表示出來;
(3)若N城位于M地正南方向,且距M地650 km,試判斷這場沙塵暴是否會侵襲到N城,如果會,在沙塵暴發生后多長時間它將侵襲到N城?如果不會,請說明理由.
【答案】(1)24;(2)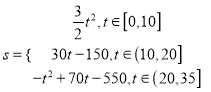 ;(3)沙塵暴發生30 h后將侵襲到N城.
;(3)沙塵暴發生30 h后將侵襲到N城.
【解析】試題分析:(1)先求出線段OA的解析式為v=4t,然后把t=10直接代入求出此時的速度,即可求出S(t)的值;(2)先分段求出速度v與時間t的函數函數關系,再分別乘以時間即可求得對應的函數S(t)的解析式;(3)先由分段函數的解析式以及對應的定義域可以求得其最大值,發現其最大值大于650,即可下結論會侵襲到N城,再把S(t)=650代入即可求出對應的t.
試題解析:解:(1)由圖像可知,當t=4時,v=3×4=12,
所以S=![]() ×4×12=24 km.
×4×12=24 km.
(2)當0≤t≤10時,S=![]() ·t·3t=
·t·3t=![]() ;
;
當10<t≤20時,S=![]() ×10×30+30(t-10)=30t-150;
×10×30+30(t-10)=30t-150;
當20<t≤35時,S=![]() ×10×30+10×30+(t-20)×30-
×10×30+10×30+(t-20)×30-![]() ×(t-20)×2(t-20)=
×(t-20)×2(t-20)=![]() .
.
綜上可知, 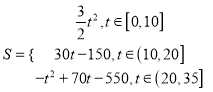 .
.
(3)因為當t∈[0,10]時,Smax=![]() ×102=150<650,
×102=150<650,
當t∈(10,20]時,Smax=30×20-150=450<650,
所以當t∈(20,35]時,令![]() ,解得
,解得![]() .因為20<t≤35,所以t=30.
.因為20<t≤35,所以t=30.
故沙塵暴發生30 h后將侵襲到N城.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】2018年1曰8日,中共中央、國務院隆重舉行國家科學技術獎勵大會,在科技界引發熱烈反響,自主創新正成為引領經濟社會發展的強勁動力.某科研單位在研發新產品的過程中發現了一種新材料,由大數據測得該產品的性能指標值![]() 與這種新材料的含量
與這種新材料的含量![]() (單位:克)的關系為:當
(單位:克)的關系為:當![]() 時,
時, ![]() 是
是![]() 的二次函數;當
的二次函數;當![]() 時,
時, ![]() .測得數據如表(部分)
.測得數據如表(部分)
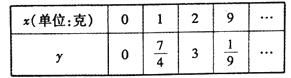
(1)求![]() 關于
關于![]() 的函數關系式
的函數關系式![]() ;
;
(2)其函數![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 及函數
及函數![]() (a,b,c∈R),若a>b>c且a+b+c=0.
(a,b,c∈R),若a>b>c且a+b+c=0.
(1)證明:f(x)的圖像與g(x)的圖像一定有兩個交點;
(2)請用反證法證明:![]() ;
;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ,
, ![]() )為奇函數,且相鄰兩對稱軸間的距離為
)為奇函數,且相鄰兩對稱軸間的距離為![]() .
.
(1)當![]() 時,求
時,求![]() 的單調遞減區間;
的單調遞減區間;
(2)將函數![]() 的圖象沿
的圖象沿![]() 軸方向向右平移
軸方向向右平移![]() 個單位長度,再把橫坐標縮短到原來的
個單位長度,再把橫坐標縮短到原來的![]() (縱坐標不變),得到函數
(縱坐標不變),得到函數![]() 的圖象.當
的圖象.當![]() 時,求函數
時,求函數![]() 的值域.
的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|a﹣3x|﹣|2+x|.
(1)若a=2,解不等式f(x)≤3;
(2)若存在實數a,使得不等式f(x)≥1﹣a+2|2+x|成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設關于某設備的使用年限![]() (年)和所支出的維修費用
(年)和所支出的維修費用![]() (萬元)有如下統計資料:
(萬元)有如下統計資料:
| 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
若由資料知, ![]() 對
對![]() 呈線性相關關系,試求:
呈線性相關關系,試求:
(1)回歸直線方程;
(2)估計使用年限為10年時,維修費用約是多少?
參考公式:回歸直線方程: ![]() .其中
.其中
(注: ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=ax+bx-cx,其中c>a>0,c>b>0.若a,b,c是△ABC的三條邊長,則下列結論正確的是______(寫出所有正確結論的序號)
①對任意的x∈(-∞,1),都有f(x)>0;
②存在x∈R,使ax,bx,cx不能構成一個三角形的三條邊長;
③若△ABC是頂角為120°的等腰三角形,則存在x∈(1,2),使f(x)=0.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com