自“釣魚島事件”,中日關系日趨緊張,不斷升級.為了積極響“保釣行動”,學校舉辦了一場保釣知識大賽,共分兩組.其中甲組滿分的有1個女生和3個男生,乙組得滿分的有2個女生和4個男生.現從得滿分的同學中,每組各任選2個同學,作為保釣行動代言人.
(1)求選出的4個同學中恰有1個女生的概率;
(2)設X為選出的4個同學中女生的個數,求X的分布列和數學期望.
【答案】
分析:(1)設“從甲組內選出的2個同學均為男同學;從乙組內選出的2個同學中,1個是男同學,1為女同學”為事件A,“從乙組內選出的2個同學均為男同學;甲組內選出的2個同學中1個是男同學,1個為女同學”為事件B,求得P(A),P(B),進而可得P(A+B);(2)可得X可能的取值為0,1,2,3,分別可得其概率,可得分布列,可得期望.
解答:解:(1)設“從甲組內選出的2個同學均為男同學;從乙組內選出的2個同學中,1個是男同學,1為女同學”為事件A,
“從乙組內選出的2個同學均為男同學;甲組內選出的2個同學中1個是男同學,1個為女同學”為事件B,
由于事件A?B互斥,且P(A)=
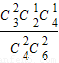
=
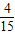
,P(B)=
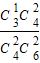
=

,
∴選出的4個同學中恰有1個女生的概率為P(A+B)=P(A)+P(B)=
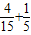
=
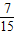
…(5分)
(2)由題意可知:X可能的取值為0,1,2,3,
由(1)可得:P(X=0)=

,P(X=1)=
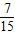
,P(X=2)=
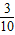
,P(X=3)=
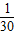
∴X的分布列為
…(10分)
∴X的數學期望:EX=
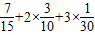
=

…(12分)
點評:本題考查離散型隨機變量的期望與方差,涉及排列組合公式的應用,屬中檔題.

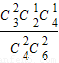 =
=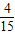 ,P(B)=
,P(B)=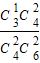 =
= ,
,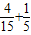 =
=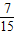 …(5分)
…(5分) ,P(X=1)=
,P(X=1)=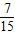 ,P(X=2)=
,P(X=2)=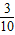 ,P(X=3)=
,P(X=3)=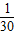

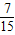
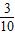
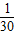
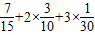 =
= …(12分)
…(12分)
