
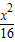 +
+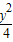 =1交于P,Q兩點,已知線段PQ的中點橫坐標為
=1交于P,Q兩點,已知線段PQ的中點橫坐標為 ,求直線l的方程.
,求直線l的方程. ,y),把P、Q坐標代入橢圓方程兩式相減,利用斜率公式及中點坐標公式可用y表示出直線斜率,再用M點坐標及中點的坐標可表示出斜率,從而得到關于y的方程,解出y后即可求得斜率,用點斜式即可求得直線方程.
,y),把P、Q坐標代入橢圓方程兩式相減,利用斜率公式及中點坐標公式可用y表示出直線斜率,再用M點坐標及中點的坐標可表示出斜率,從而得到關于y的方程,解出y后即可求得斜率,用點斜式即可求得直線方程. ,y),則x1+x2=1,y1+y2=2y,
,y),則x1+x2=1,y1+y2=2y,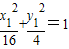 ①,
①,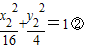 ,
,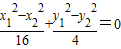 ,即
,即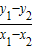 =-
=-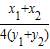 =-
=-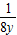 ,
,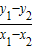 =
=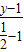 ,
,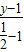 =-
=-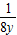 ,解得
,解得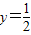
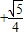 ,
,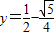 ,
,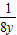 =1±
=1±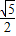 ,
,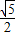 )(x-1)或y-1=(1-
)(x-1)或y-1=(1-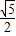 )(x-1),即y=(1+
)(x-1),即y=(1+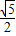 )(x-1)+1或y=(1-
)(x-1)+1或y=(1-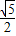 )(x-1)+1.
)(x-1)+1.

 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com