如圖，多面體ABCDEF中，已知面ABCD是邊長為3的正方形，EF∥AB，
，EF與面AC的距離為2，則該多面體的體積為 ( )
(A) 
(B) 5 (C) 6 (D) 
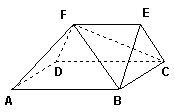
解法1：連BE和CF，多面體分割為一個四棱錐E－ABCD和一個三棱錐E－BCF．因為EF到面AC的距離為2，ABCD是邊長為3的正方形，所以四棱錐E－ABCD的體積
而多面體ABCDEF的體積V>V1， 從而排除(A)、(B)、(C)得答案為(D)． 解法2：解法1采用了估值的方法，也可以準確算出VE－BCF(計算時不妨設EF⊥面BCF)
因此多面體ABCDEF的體積
答案選(D) 解法3：
延長EF至G，使FG=AB．則AGD－BFC是一個三棱柱．因為EF (即FG)到面AC的距離為2，ABCD是邊長為3的正方形．所以這個三棱柱的體積為(計算時不妨設面BCF⊥面AC) 三棱錐E－AGD的體積為
所以多面體ABCDEF的體積
|
期末100分闖關海淀考王系列答案
小學能力測試卷系列答案科目：高中數學 來源： 題型：
| AK |
| AE |
查看答案和解析>>
科目：高中數學 來源：2010-2011學年東北師大附中、哈師大附中、遼寧實驗中學高三第二次模擬考試數學理卷 題型：解答題
（（本小題滿分12分）
如圖，多面體ABCD—EFG中，底面ABCD為正方形，GD//FC//AE，AE⊥平面ABCD，其正視圖、俯視圖如下：
（I）求證：平面AEF⊥平面BDG；
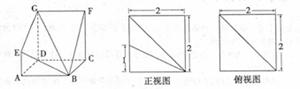
（II）若存在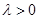
使得
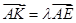，二面角A—BG—K的大小為
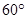，求
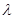的值。
查看答案和解析>>
科目：高中數學 來源：2010-2011年浙江省高二下學期期中考試理數試題 題型：選擇題
（（本小題滿分12分）
如圖，多面體ABCD—EFG中，底面ABCD為正方形，GD//FC//AE，AE⊥平面ABCD，其正視圖、俯視圖如下：
（I）求證：平面AEF⊥平面BDG；
（II）若存在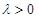
使得
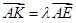，二面角A—BG—K的大小為
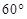，求
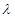的值。
查看答案和解析>>
科目：高中數學 來源：2010-2011年東北師大附中、哈師大附中、遼寧實驗中學高二第二次考試數學理卷 題型：解答題
（本小題滿分12分）
如圖，多面體ABCD—EFG中，底面ABCD為正方形，GD//FC//AE，AE⊥平面ABCD，其正視圖、俯視圖如下：
（I）求證：平面AEF⊥平面BDG；
（II）若存在
使得
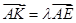，二面角A—BG—K的大小為
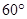，求
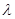的值。
查看答案和解析>>
科目：高中數學 來源：模擬題 題型：解答題
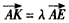，KF與平面ABG所成角為30°，求λ的值。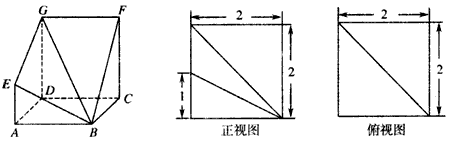 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，
,
．
．
．
