【題目】在正方體
中，
是棱
的中點，
是側面
內的動點,且
與平面
的垂線垂直，如圖所示，下列說法不正確的序號為__________
①點的軌跡是一條線段.②與
是異面直線.
③與
不可能平行.④三棱錐
的體積為定值.
【答案】③
【解析】
分別根據線面平行的性質定理以及異面直線的定義，以及體積公式分別進行判斷.
對于①，設平面
與直線
交于點
，連接
，則為的中點..
分別取
的中點
，連接
，
則
平面
，
平面.
所以
平面，同理可得
平面
是平面
內的相交直線.
所以平面
平面，
由
與平面的垂線垂直,則
平面，可得直線
平面.
即點
是線段
上的動點，所以①正確.
對于②，由①有點在線段上，所以
三點在側面
內.
假設與
不是異面直線，則
四點共面,則他們共面于側面內.
這與在正方體中，顯然
產生矛盾，所以假設不成立.
故與是異面直線，故②正確.
對于③，當與
重合時，
，所以③錯誤.
對于④，
,
,則平面
.
則點到平面的距離等于點(或點
)到平面的距離.
設點(或點)到平面的距離為
.
則
，即
.
在正方體中，
，
，
均為定值，所以為定值.
點到平面的距離為定值，又為定值.
所以
的體積為定值,故④正確.
故答案為：③.
陽光課堂課時優化作業系列答案科目：高中數學 來源： 題型：
【題目】有一塊半圓形的空地，直徑
米，政府計劃在空地上建一個形狀為等腰梯形的花圃
，如圖所示，其中
為圓心，
，
在半圓上，其余為綠化部分，設
.
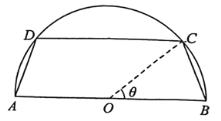
（1）記花圃的面積為
，求的最大值；
（2）若花圃的造價為10元/米，在花圃的邊
、
處鋪設具有美化效果的灌溉管道，鋪設費用為500元/米，兩腰、不鋪設，求
滿足什么條件時，會使總造價最大.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在平面直角坐標系，將曲線
上的每一個點的橫坐標保持不變，縱坐標縮短為原來的
，得到曲線
，以坐標原點
為極點， 
軸的正半軸為極軸，建立極坐標系， 
的極坐標方程為
．
（Ⅰ）求曲線
的參數方程；
（Ⅱ）過原點
且關于
軸對稱的兩條直線
與
分別交曲線
于
、
和
、
，且點
在第一象限，當四邊形
的周長最大時，求直線
的普通方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】四色猜想是世界三大數學猜想之一，1976年數學家阿佩爾與哈肯證明，稱為四色定理.其內容是：“任意一張平面地圖只用四種顏色就能使具有共同邊界的國家涂上不同的顏色.”用數學語言表示為“將平面任意地細分為不相重疊的區域，每一個區域總可以用
，
，
，
四個數字之一標記，而不會使相鄰的兩個區域得到相同的數字.”如圖，網格紙上小正方形的邊長為，粗實線圍城的各區域上分別標有數字，，，的四色地圖符合四色定理，區域
和區域
標記的數字丟失.若在該四色地圖上隨機取一點，則恰好取在標記為的區域的概率所有可能值中，最大的是（ ）
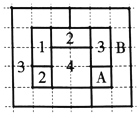
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】[2019·濰坊期末]某鋼鐵加工廠新生產一批鋼管，為了了解這批產品的質量狀況，檢驗員隨機抽取了100件鋼管作為樣本進行檢測，將它們的內徑尺寸作為質量指標值，由檢測結果得如下頻率分布表和頻率分布直方圖：
分組 | 頻數 | 頻率 |
25.05～25.15 | 2 | 0.02 |
25.15～25.25 | ||
25.25～25.35 | 18 | |
25.35～25.45 | ||
25.45～25.55 | ||
25.55～25.65 | 10 | 0.1 |
25.65～25.75 | 3 | 0.03 |
合計 | 100 | 1 |
（1）求
，
；
（2）根據質量標準規定：鋼管內徑尺寸大于等于25.75或小于25.15為不合格，鋼管尺寸在
或
為合格等級，鋼管尺寸在
為優秀等級，鋼管的檢測費用為0.5元/根．
（i）若從
和
的5件樣品中隨機抽取2根，求至少有一根鋼管為合格的概率；
（ii）若這批鋼管共有2000根，把樣本的頻率作為這批鋼管的頻率，有兩種銷售方案：
①對該批剩余鋼管不再進行檢測，所有鋼管均以45元/根售出；
②對該批剩余鋼管一一進行檢測，不合格產品不銷售，合格等級的鋼管50元/根，優等鋼管60元/根．
請你為該企業選擇最好的銷售方案，并說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】建設生態文明，是關系人民福祉，關乎民族未來的長遠大計.某市通宵營業的大型商場，為響應節能減排的號召，在氣溫超過
時，才開放中央空調降溫，否則關閉中央空調.如圖是該市夏季一天的氣溫（單位：
）隨時間（
，單位：小時）的大致變化曲線，若該曲線近似的滿足函數
關系.
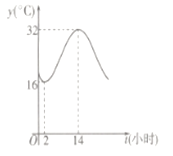
（1）求函數
的表達式；
（2）請根據（1）的結論，判斷該商場的中央空調應在本天內何時開啟？何時關閉？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某種新產品投放市場一段時間后，經過調研獲得了時間
（天數）與銷售單價
（元）的一組數據，且做了一定的數據處理（如表），并作出了散點圖（如圖）
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中
，
.
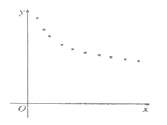
（1）根據散點圖判斷，
與
哪一個更適宜作價格關于時間的回歸方程類型？（不必說明理由）
（2）根據判斷結果和表中數據，建立關于的回歸方程；
（3）若該產品的日銷售量
（件）與時間的函數關系為
（
），求該產品投放市場第幾天的銷售額最高？最高為多少元？（結果保留整數）
附：對于一組數據
，
，
，
，
，其回歸直線
的斜率和截距的最小二乘估計分別為
，
.
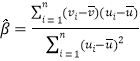查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】瑞士著名數學家歐拉在1765年提出定理：三角形的外心、重心、垂心位于同一直線上.這條直線被后人稱為三角形的“歐拉線”.在平面直角坐標系中作△ABC，AB＝AC＝4，點B(－1，3)，點C(4，－2)，且其“歐拉線”與圓M：
相切，則下列結論正確的是（ ）
A.圓M上點到直線
的最小距離為2
B.圓M上點到直線的最大距離為3
C.若點（x，y）在圓M上，則
的最小值是
D.圓
與圓M有公共點，則a的取值范圍是
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
