
【題目】如圖,四棱錐![]() 中,底面是以
中,底面是以![]() 為中心的菱形,
為中心的菱形,![]() 底面
底面![]() 為
為![]() 上一點,且
上一點,且![]() .
.
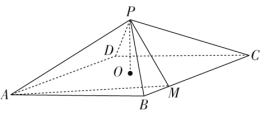
(1)求![]() 的長;
的長;
(2)求二面角![]() 的余弦值.
的余弦值.
 勵耘書業暑假銜接寧波出版社系列答案
勵耘書業暑假銜接寧波出版社系列答案科目:高中數學 來源: 題型:
【題目】甲同學參加化學競賽初賽,考試分為筆試、口試、實驗三個項目,各單項通過考試的概率依次為![]() 、
、![]() 、
、![]() ,筆試、口試、實驗通過考試分別記4分、2分、4分,沒通過的項目記0分,各項成績互不影響.
,筆試、口試、實驗通過考試分別記4分、2分、4分,沒通過的項目記0分,各項成績互不影響.
(Ⅰ)若規定總分不低于8分即可進入復賽,求甲同學進入復賽的概率;
(Ⅱ)記三個項目中通過考試的個數為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某市建有貫穿東西和南北的兩條垂直公路![]() ,
,![]() ,在它們交叉路口點
,在它們交叉路口點![]() 處的東北方向建有一個荷花池,荷花池的外圍是一條環形公路,荷花池中的固定觀景臺
處的東北方向建有一個荷花池,荷花池的外圍是一條環形公路,荷花池中的固定觀景臺![]() 位于兩條垂直公路的角平分線
位于兩條垂直公路的角平分線![]() 上,
上,![]() 與環形公路的交點記作
與環形公路的交點記作![]() .游客游覽荷花池時,需沿公路
.游客游覽荷花池時,需沿公路![]() 先到達環形公路
先到達環形公路![]() 處.為了分流游客,方便游客游覽荷花池,計劃從靠近公路
處.為了分流游客,方便游客游覽荷花池,計劃從靠近公路![]() ,
,![]() 的環形公路上選
的環形公路上選![]() ,
,![]() 兩處(
兩處(![]() ,
,![]() 關于直線
關于直線![]() 對稱)修建直達觀景臺
對稱)修建直達觀景臺![]() 的玻璃棧道
的玻璃棧道![]() ,
,![]() .以
.以![]() ,
,![]() 所在的直線為
所在的直線為![]() ,
,![]() 軸建立平面直角坐標系
軸建立平面直角坐標系![]() ,靠近公路
,靠近公路![]() ,
,![]() 的環形公路可用曲線
的環形公路可用曲線![]() 近似表示,曲線
近似表示,曲線![]() 符合函數
符合函數![]() .
.
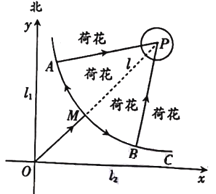
(1)若![]() 百米,點
百米,點![]() 到
到![]() 的垂直距離為1百米,求玻璃棧道
的垂直距離為1百米,求玻璃棧道![]() 的總長度;
的總長度;
(2)若要使得玻璃棧道![]() 的總長度最小為
的總長度最小為![]() 百米,求觀景臺
百米,求觀景臺![]() 的位置.
的位置.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某保險公司對一個擁有20000人的企業推出一款意外險產品,每年每位職工只要交少量保費,發生意外后可一次性獲得若干賠償金,保險公司把企業的所有崗位共分為![]() 三類工種,從事這三類工種的人數分別為12000,6000,2000,由歷史數據統計出三類工種的賠付頻率如下表(并以此估計賠付概率):
三類工種,從事這三類工種的人數分別為12000,6000,2000,由歷史數據統計出三類工種的賠付頻率如下表(并以此估計賠付概率):
已知![]() 三類工種職工每人每年保費分別為25元、25元、40元,出險后的賠償金額分別為100萬元、100萬元、50萬元,保險公司在開展此項業務過程中的固定支出為每年10萬元.
三類工種職工每人每年保費分別為25元、25元、40元,出險后的賠償金額分別為100萬元、100萬元、50萬元,保險公司在開展此項業務過程中的固定支出為每年10萬元.
(1)求保險公司在該業務所或利潤的期望值;
(2)現有如下兩個方案供企業選擇:
方案1:企業不與保險公司合作,職工不交保險,出意外企業自行拿出與保險公司提供的等額賠償金賠償付給意外職工,企業開展這項工作的固定支出為每年12萬元;
方案2:企業與保險公司合作,企業負責職工保費的70%,職工個人負責保費的30%,出險后賠償金由保險公司賠付,企業無額外專項開支.
請根據企業成本差異給出選擇合適方案的建議.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是邊長為2的菱形,
是邊長為2的菱形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,點
,點![]() 為棱
為棱![]() 的中點.
的中點.

(Ⅰ)在棱![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 平面
平面![]() ,并說明理由;
,并說明理由;
(Ⅱ)當二面角![]() 的余弦值為
的余弦值為![]() 時,求直線
時,求直線![]() 與平面
與平面![]() 所成的角.
所成的角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】基于移動網絡技術的共享單車被稱為“新四大發明”之一,短時間內就風靡全國,給人們帶來新的出行體驗,某共享單車運營公司的市場研究人員為了了解公司的經營狀況,對公司最近6個月的市場占有率![]() 進行了統計,結果如下表:
進行了統計,結果如下表:
月份 | 2018.11 | 2018.12 | 2019.01 | 2019.02 | 2019.03 | 2019.04 |
月份代碼 | 1 | 2 | 3 | 4 | 5 | 6 |
| 11 | 13 | 16 | 15 | 20 | 21 |
(1)請用相關系數說明能否用線性回歸模型擬合![]() 與月份代碼
與月份代碼![]() 之間的關系.如果能,請計算出
之間的關系.如果能,請計算出![]() 關于
關于![]() 的線性回歸方程,如果不能,請說明理由;
的線性回歸方程,如果不能,請說明理由;
(2)根據調研數據,公司決定再采購一批單車擴大市場,從成本1000元/輛的![]() 型車和800元/輛的
型車和800元/輛的![]() 型車中選購一種,兩款單車使用壽命頻數如下表:
型車中選購一種,兩款單車使用壽命頻數如下表:
| 1年 | 2年 | 3年 | 4年 | 總計 |
| 10 | 30 | 40 | 20 | 100 |
| 15 | 40 | 35 | 10 | 100 |
經測算,平均每輛單車每年能為公司帶來500元的收入,不考慮除采購成本以外的其它成本,假設每輛單車的使用壽命都是整數年,用頻率估計每輛車使用壽命的概率,以平均每輛單車所產生的利潤的估計值為決策依據,如果你是公司負責人,會選擇哪款車型?
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() .
.
參考公式:相關系數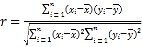 ,
,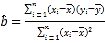 ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com