
 ,0)的距離與P到直線
,0)的距離與P到直線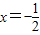 距離相等
距離相等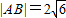 ,求直線l的方程;
,求直線l的方程;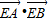 恒為定值?若存在,求出E的坐標及定值;若不存在,請說明理由.
恒為定值?若存在,求出E的坐標及定值;若不存在,請說明理由. ,0)的距離與P到直線
,0)的距離與P到直線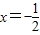 距離相等
距離相等 ,0)為焦點的拋物線,方程為y2=2x;
,0)為焦點的拋物線,方程為y2=2x;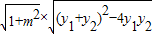 =
=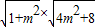 =2
=2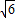
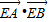 =(x1-a)(x2-a)+y1y2=-2am2+(1-a)2-2恒為定值
=(x1-a)(x2-a)+y1y2=-2am2+(1-a)2-2恒為定值

科目:高中數學 來源: 題型:
| QP |
| QF |
| FP |
| FQ |
| FA |
| FB |
查看答案和解析>>
科目:高中數學 來源: 題型:
| PC |
| 1 |
| 2 |
| PQ |
| PC |
| 1 |
| 2 |
| PQ |
| PE |
| PF |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| PC |
| 1 |
| 2 |
| PQ |
| PC |
| 1 |
| 2 |
| PQ |
| PE |
| PF |
查看答案和解析>>
科目:高中數學 來源:2013年高考數學復習卷C(四)(解析版) 題型:解答題
 .
. 的最大值.
的最大值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com